Euclides - Elementos Libros X-XIII
Aquí puedes leer online Euclides - Elementos Libros X-XIII texto completo del libro (historia completa) en español de forma gratuita. Descargue pdf y epub, obtenga significado, portada y reseñas sobre este libro electrónico. Año: 0300, Editor: ePubLibre, Género: Historia. Descripción de la obra, (prefacio), así como las revisiones están disponibles. La mejor biblioteca de literatura LitFox.es creado para los amantes de la buena lectura y ofrece una amplia selección de géneros:
Novela romántica
Ciencia ficción
Aventura
Detective
Ciencia
Historia
Hogar y familia
Prosa
Arte
Política
Ordenador
No ficción
Religión
Negocios
Niños
Elija una categoría favorita y encuentre realmente lee libros que valgan la pena. Disfrute de la inmersión en el mundo de la imaginación, sienta las emociones de los personajes o aprenda algo nuevo para usted, haga un descubrimiento fascinante.
Elementos Libros X-XIII: resumen, descripción y anotación
Ofrecemos leer una anotación, descripción, resumen o prefacio (depende de lo que el autor del libro "Elementos Libros X-XIII" escribió él mismo). Si no ha encontrado la información necesaria sobre el libro — escribe en los comentarios, intentaremos encontrarlo.
Euclides: otros libros del autor
¿Quién escribió Elementos Libros X-XIII? Averigüe el apellido, el nombre del autor del libro y una lista de todas las obras del autor por series.
Elementos Libros X-XIII — leer online gratis el libro completo
A continuación se muestra el texto del libro, dividido por páginas. Sistema guardar el lugar de la última página leída, le permite leer cómodamente el libro" Elementos Libros X-XIII " online de forma gratuita, sin tener que buscar de nuevo cada vez donde lo dejaste. Poner un marcador, y puede ir a la página donde terminó de leer en cualquier momento.
Tamaño de fuente:
Intervalo:
Marcador:
DEFINICIONES
| 1. | Se llaman magnitudes conmensurables aquellas que se miden con la misma medida, e inconmensurables aquellas de las que no es posible que haya una medida común. |
| 2. | Las líneas rectas son conmensurables en cuadrado cuando sus cuadrados se miden con la misma área, e inconmensurables cuando no es posible que sus cuadrados tengan un área como medida común. |
| 3. | Dados estos supuestos, se demuestra que hay un número infinito de rectas respectivamente conmensurables e inconmensurables, unas sólo en longitud y otras también en cuadrado con una recta determinada. Llámese entonces racionalmente expresable la recta determinada; y las conmensurables con ella, bien en longitud y en cuadrado, bien sólo en cuadrado, racionalmente expresables y las inconmensurables con ella llámense no racionalmente expresables. |
| 4. | Y el cuadrado de la recta determinada (llámese) racionalmente expresable, y los cuadrados conmensurables con éste racionalmente expresables; pero los inconmensurables con él llámense no racionalmente expresables; y las rectas que los producen (llámense) no racionalmente expresablas, a saber, si fueran cuadrados, los propios lados y si fueran otras figuras rectilíneas, aquellas (rectas) que construyan cuadrados iguales a ellos. |
PROPOSICIÓN 1
Dadas dos magnitudes desiguales, si se quita de la mayor una (magnitud) mayor que su mitad y, de la que queda, una magnitud mayor que su mitad y así sucesivamente, quedará una magnitud que será menor que la magnitud menor dada.
Sean AB, Γ dos magnitudes desiguales de las cuales AB es la mayor.
Digo que, si se quita de AB una (magnitud) mayor que su mitad y de la (magnitud) restante, una (magnitud) mayor que su mitad, y así sucesivamente, quedará una magnitud que será menor que la magnitud Γ.
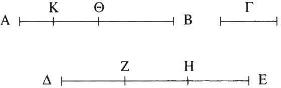
Pues Γ multiplicada será alguna vez mayor que AB [V Def. 4]. Multiplíquese y sea ΔE un múltiplo de Γ mayor que AB; divídase ΔE en ΔZ, ZH, HE iguales a Γ, y de AB quítese BΘ mayor que su mitad, y de AΘ (quítese) ΘK mayor que su mitad, y así sucesivamente hasta que las divisiones de AB lleguen a ser iguales en número a las divisiones de ΔE.
Sean, pues, AK, KΘ, ΘB divisiones que son iguales en número a las (divisiones) ΔZ, ZH, HE; ahora bien, dado que ΔE es mayor que AB y que de ΔE se ha quitado la (magnitud) EH menor que su mitad y de AB la (magnitud) BΘ mayor que su mitad, entonces la magnitud restante HΔ es mayor que la (magnitud) restante ΘA. Y dado que HΔ es mayor que ΘA y se ha quitado de HΔ su mitad HZ y de ΘA una (magnitud) ΘK mayor que su mitad, entonces la (magnitud) restante ΔZ es mayor que la (magnitud) restante AK. Pero ΔZ es igual a Γ; luego es mayor que AK. Por tanto, AK es menor que Γ.
Por consiguiente, de la magnitud AB queda la magnitud AK que es menor que la magnitud dada Γ. Q. E. D. De manera semejante demostraríamos que (esto ocurre) también si se quita la mitad.
PROPOSICIÓN 2
Si al restar continua y sucesivamente la menor de la mayor de dos magnitudes desiguales, la restante nunca mide a la anterior, las magnitudes serán inconmensurables.
Habiendo, pues, dos magnitudes desiguales AB, ΓΔ y (siendo) AB la menor, al restar sucesivamente la menor de la mayor, no mida nunca la (magnitud) restante a la anterior a ella.
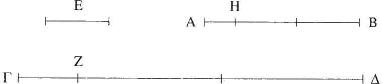
Digo que las magnitudes AB, ΓΔ son inconmensurables.
Pues, si son conmensurables, alguna magnitud las medirá. Mídalas (una magnitud), si es posible, y sea E; y AB, al medir a ZΔ, deje la magnitud ΓZ menor que ella, y ΓZ, al medir a BH, deje AH menor que ella, y repítase así sucesivamente hasta que quede una magnitud que sea menor que E. Sea así y quede AH menor que E. Así pues, como E mide a AB y AB mide a ΔZ, entonces E también medirá a ZΔ. Pero mide también a la magnitud entera ΓΔ; luego medirá también a la magnitud restante ΓZ. Ahora bien, ΓZ mide a BH; entonces E también mide a BH. Pero mide también a la (magnitud) entera AB; así que medirá también a la (magnitud) restante AH, la mayor a la menor; lo cual es imposible. Luego ninguna magnitud medirá a las magnitudes AB, ΓΔ; por tanto, las magnitudes AB, ΓΔ son inconmensurables [X Def. 1].
Por consiguiente, si de dos magnitudes desiguales…, etc..
PROPOSICIÓN 3
Dadas dos magnitudes conmensurables, hallar su medida común máxima.
Sean AB, ΓΔ dos magnitudes dadas conmensurables, de las cuales AB sea la menor.
Así pues, hay que hallar la medida común máxima de AB, ΓΔ.
Pues bien, AB o mide a ΓΔ o no la mide. Si, en efecto, la mide y se mide también a sí misma, entonces AB es una medida común de AB, ΓΔ; y está claro que también es la mayor. Porque no medirá a AB ninguna magnitud mayor que AB.
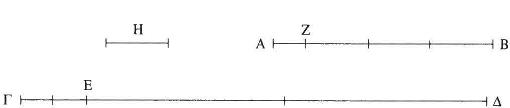
Pero ahora no mida AB a ΓΔ y, al restar continua y sucesivamente la menor de la mayor, la (magnitud) restante medirá alguna vez a la anterior a ella, porque AB, ΓΔ no son inconmensurables [X 2]; y AB, al medir a EΔ, deje la (magnitud) EΓ menor que ella, y EΓ, al medir a ZB, deje la (magnitud) AZ menor que ella y mida AZ a ΓE.
Como, en efecto, AZ mide a ΓE, mientras que ΓE mide a ZB, entonces AZ medirá también a ZB. Pero también se mide a sí misma; luego AZ medirá también a la (magnitud) entera AB. Ahora bien, AB mide a ΔE; entonces AZ medirá también a EΔ. Pero mide también a ΓE; luego mide también a la (magnitud) entera ΓΔ; por tanto, AZ es una medida común de AB, ΓΔ.
Digo ahora que también es la mayor. Pues, si no, habrá una magnitud mayor que AZ que medirá a AB, ΓΔ. Sea H. Así pues, dado que H mide a AB, mientras que AB mide a EΔ, entonces H medirá a EΔ. Pero mide también a la (magnitud) entera ΓΔ; luego H medirá también a la (magnitud) restante ΓE. Pero ΓE mide a ZB; luego H medirá también a ZB. Pero también mide a la (magnitud) entera AB y medirá también a la (magnitud) restante AZ, la mayor a la menor; lo cual es imposible. Luego ninguna magnitud mayor que AZ medirá a AB, ΓΔ; por tanto AZ es la medida común máxima de AB, ΓΔ.
Por consiguiente, se ha hallado la medida común máxima, AZ, de las dos magnitudes dadas AB, ΓΔ. Q. E. D.
Porisma:
A partir de esto queda claro que, si una magnitud mide a dos magnitudes, medirá también a su medida común máxima.
PROPOSICIÓN 4
Dadas tres magnitudes conmensurables, hallar su medida común máxima.
Sean A, B, Γ las tres magnitudes conmensurables dadas.
Así pues, hay que hallar la medida común máxima de A, B, Γ.
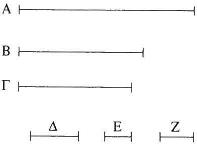
Tómese, pues, la medida común máxima de A, B y sea Δ [X 3]. Pues bien, o Δ mide a Γ o no la mide. En primer lugar, mídala. Así pues Δ mide a Γ, y mide también a A, B, entonces Δ mide a A, B, Γ; por tanto Δ es una medida común de A, B, Γ. Y está claro que también la mayor, porque una magnitud mayor que la magnitud Δ no mide a A, B.
No mida ahora Δ a Γ.
Digo en primer lugar que Γ, Δ son conmensurables.
Porque como A, B, Γ son conmensurables, las medirá alguna magnitud que evidentemente medirá también a A, B; de modo que la medida común máxima de A, B medirá también a Δ. Y mide también a Γ; de modo que la antedicha magnitud medirá también a Δ, la medida común máxima de A, B [X 3 Por.], luego Γ, Δ son conmensurables.
Tamaño de fuente:
Intervalo:
Marcador:
Libros similares «Elementos Libros X-XIII»
Mira libros similares a Elementos Libros X-XIII. Hemos seleccionado literatura similar en nombre y significado con la esperanza de proporcionar lectores con más opciones para encontrar obras nuevas, interesantes y aún no leídas.
Discusión, reseñas del libro Elementos Libros X-XIII y solo las opiniones de los lectores. Deja tus comentarios, escribe lo que piensas sobre la obra, su significado o los personajes principales. Especifica exactamente lo que te gustó y lo que no te gustó, y por qué crees que sí.













