Euclides - Elementos Libros V-IX
Aquí puedes leer online Euclides - Elementos Libros V-IX texto completo del libro (historia completa) en español de forma gratuita. Descargue pdf y epub, obtenga significado, portada y reseñas sobre este libro electrónico. Año: 0300, Editor: ePubLibre, Género: Historia. Descripción de la obra, (prefacio), así como las revisiones están disponibles. La mejor biblioteca de literatura LitFox.es creado para los amantes de la buena lectura y ofrece una amplia selección de géneros:
Novela romántica
Ciencia ficción
Aventura
Detective
Ciencia
Historia
Hogar y familia
Prosa
Arte
Política
Ordenador
No ficción
Religión
Negocios
Niños
Elija una categoría favorita y encuentre realmente lee libros que valgan la pena. Disfrute de la inmersión en el mundo de la imaginación, sienta las emociones de los personajes o aprenda algo nuevo para usted, haga un descubrimiento fascinante.
Elementos Libros V-IX: resumen, descripción y anotación
Ofrecemos leer una anotación, descripción, resumen o prefacio (depende de lo que el autor del libro "Elementos Libros V-IX" escribió él mismo). Si no ha encontrado la información necesaria sobre el libro — escribe en los comentarios, intentaremos encontrarlo.
Euclides: otros libros del autor
¿Quién escribió Elementos Libros V-IX? Averigüe el apellido, el nombre del autor del libro y una lista de todas las obras del autor por series.
Elementos Libros V-IX — leer online gratis el libro completo
A continuación se muestra el texto del libro, dividido por páginas. Sistema guardar el lugar de la última página leída, le permite leer cómodamente el libro" Elementos Libros V-IX " online de forma gratuita, sin tener que buscar de nuevo cada vez donde lo dejaste. Poner un marcador, y puede ir a la página donde terminó de leer en cualquier momento.
Tamaño de fuente:
Intervalo:
Marcador:
DEFINICIONES
| 1. | Una magnitud es parte de una magnitud, la menor de la mayor, cuando mide a la mayor. |
| 2. | Y la mayor es múltiplo de la menor cuando es medida por la menor. |
| 3. | Una razón es determinada relación con respecto a su tamaño entre dos magnitudes homogéneas. |
| 4. | Se dice que guardan razón entre sí las magnitudes que, al multiplicarse, pueden exceder una a otra. |
| 5. | Se dice que una primera magnitud guarda la misma razón. |
| 6. | Llámense proporcionales las magnitudes que guardan la misma razón. |
| 7. | Entre los equimúltiplos, cuando el múltiplo de la primera excede al múltiplo de la segunda pero el múltiplo de la tercera no excede al múltiplo de la cuarta, entonces se dice que la primera guarda con la segunda una razón mayor que la tercera con la cuarta. |
| 8. | Una proporción entre tres términos es la menor posible. |
| 9. | Cuando tres magnitudes son proporcionales, se dice que la primera guarda con la tercera una razón duplicada de la que (guarda) con la segunda. |
| 10. | Cuando cuatro magnitudes son proporcionales, se dice que la primera guarda con la cuarta una razón triplicada de la que (guarda) con la segunda, y así siempre, sucesivamente, sea cual fuere la proporción. |
| 11. | Se llaman magnitudes correspondientes las antecedentes en relación con las antecedentes y las consecuentes con las consecuentes. |
| 12. | Una razón por alternancia consiste en tomar el antecedente en relación con el antecedente y el consecuente en relación con el consecuente. |
| 13. | Una razón por inversión consiste en tomar el consecuente como antecedente en relación con el antecedente como consecuente. |
| 14. | La composición de una razón consiste en tomar el antecedente junto con el consecuente como una sola (magnitud) en relación con el propio consecuente. |
| 15. | La separación de una razón consiste en tomar el exceso por el que el antecedente excede al consecuente en relación con el propio consecuente. |
| 16. | La conversión de una razón consiste en tomar el antecedente en relación con el exceso por el que el antecedente excede al consecuente. |
| 17. | Una razón por igualdad. |
| 18. | Una proporción perturbada. |
PROPOSICIÓN 1
Si hay un número cualquiera de magnitudes respectivamente equimúltiplos de cualesquiera otras magnitudes iguales en número, cuantas veces una sea múltiplo de otra, tantas veces lo serán todas de todas.
Sean un número cualquiera de magnitudes AB, ΓΔ respectivamente equimúltiplos de cualesquiera otras magnitudes E, Z iguales en número.
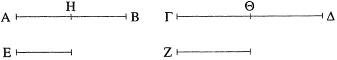
Digo que, cuantas veces AB sea múltiplo de E, tantas veces lo serán también AB, ΓΔ de E, Z.
Pues dado que AB es equimúltiplo de E y ΓΔ de Z, entonces, cuantas magnitudes iguales a E hay en AB, tantas hay también en ΓΔ iguales a Z. Divídase AB en las magnitudes AH, HB iguales a E y ΓΔ en las (magnitudes) ΓΘ, ΘΔ iguales a Z; entonces el número de las (magnitudes) AH, HB será igual al número de las (magnitudes) ΓΘ, ΘΔ. Ahora bien, como AH es igual a E y ΓΘ a Z, entonces AH es igual a E y AH, ΓΘ a E, Z. Por lo mismo, HB es igual a E y HB, ΘΔ a E, Z; por tanto, cuantas (magnitudes) hay en AB iguales a E, tantas hay también en AB, ΓΔ iguales a E, Z; luego cuantas veces sea AB múltiplo de E, tantas veces lo serán también AB, ΓΔ de E, Z.
Por consiguiente, si hay un número cualquiera de magnitudes respectivamente equimúltiplos de cualesquiera otras magnitudes iguales en número, cuantas veces una sea múltiplo de otra, tantas veces lo serán también todas de todas. Q. E. D.
PROPOSICIÓN 2
Si una primera (magnitud) es el mismo múltiplo de una segunda que una tercera de una cuarta, y una quinta es también el mismo múltiplo de la segunda que una sexta de la cuarta, la suma de la primera y la quinta será el mismo múltiplo de la segunda que la suma de la tercera y la sexta de la cuarta.
Pues sea la primera (magnitud), AB, el mismo múltiplo de la segunda, Γ, que la tercera, ΔE, de la cuarta, Z, y sea la quinta, BH, el mismo múltiplo de la segunda, Γ, que la sexta, EΘ, de la cuarta, Z.
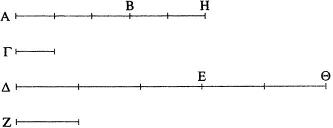
Digo que la suma de la primera y la quinta, AH, es el mismo múltiplo de la segunda, Γ, que la (suma de) la tercera y la sexta, ΔΘ, de la cuarta, Z.
Pues, dado que AB es el mismo múltiplo de Γ que ΔE de Z, entonces, cuantas (magnitudes) hay en AB iguales a Γ, tantas hay también en ΔE iguales a Z. Y, por lo mismo, cuantas (magnitudes) hay en BH iguales a Γ, tantas hay también en EΘ iguales a Z; así pues, cuantas (magnitudes) hay en la (magnitud) entera AH iguales a Γ, tantas hay también en la (magnitud) entera ΔΘ iguales a Z; por tanto, cuantas veces AH es múltiplo de Γ, tantas veces lo será ΔΘ de Z. Luego la suma de la primera y la quinta, AH, será también el mismo múltiplo de la segunda, Γ, que la (suma de) la tercera y la sexta, ΔΘ, de la cuarta, Z.
Por consiguiente, si una primera (magnitud) es el mismo múltiplo de una segunda que una tercera de una cuarta y una quinta es también el mismo múltiplo de la segunda que una sexta de la cuarta, la suma de la primera y la quinta será el mismo múltiplo de la segunda que la suma de la tercera y la sexta de la cuarta. Q. E. D.
PROPOSICIÓN 3
Si una primera (magnitud) es el mismo múltiplo de una segunda que una tercera de una cuarta, y se toman equimúltiplos de la primera y la tercera, también por igualdad cada una de las dos (magnitudes) tomadas serán equimúltiplos, respectivamente, una de la segunda, y la otra de la cuarta.
Pues sea la primera, A, el mismo múltiplo de la segunda, B, que la tercera, Γ, de la cuarta, Δ, y tómense los equimúltiplos EZ, HΘ de A, Γ.
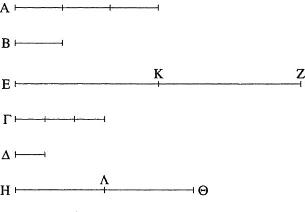
Digo que EZ es el mismo múltiplo de B que HΘ de Δ.
Pues dado que EZ es el mismo múltiplo de A que EZ de Γ, entonces, cuantas (magnitudes) hay en EZ iguales a A, tantas hay también en HΘ iguales a Γ. Divídase EZ en las magnitudes EK, KZ iguales a A, y HΘ en las (magnitudes) HΛ, ΛΘ iguales a Γ. Entonces el número de las (magnitudes) EK, KZ será igual al número de las (magnitudes) HΛ, ΛΘ. Y puesto que A es el mismo múltiplo de B que Γ de Δ, mientras que EK es igual a A y HΛ a Γ, entonces EK es el mismo múltiplo de B que HΛ de Δ. Por lo mismo KZ es el mismo múltiplo de B que ΛΘ de Δ. Así pues, dado que la primera, EK, es el mismo múltiplo de la segunda, B, que la tercera, HΛ, de la cuarta, Δ, y la quinta, KZ, también es el mismo múltiplo de la segunda, B, que la sexta, ΛΘ, de la cuarta, Δ; entonces la suma de la primera y la quinta, EZ, es también el mismo múltiplo de la segunda, B, que la (suma de) la tercera y la sexta, HΘ, de la cuarta, Δ [V, 2].
Por consiguiente, si una primera magnitud es el mismo múltiplo de una segunda que una tercera de una cuarta, y se toman equimúltiplos de la primera y la tercera, también, por igualdad, cada una de las dos (magnitudes) tomadas serán equimúltiplos, respectivamente, una de la segunda y la otra de la cuarta. Q. E. D.
PROPOSICIÓN 4
Si una primera (magnitud) guarda la misma razón con una segunda que una tercera con una cuarta, cualesquiera equimúltiplos de la primera y la tercera guardarán la misma razón con cualesquiera equimúltiplos de la segunda y la cuarta respectivamente, tomados en el orden correspondiente.
Tamaño de fuente:
Intervalo:
Marcador:
Libros similares «Elementos Libros V-IX»
Mira libros similares a Elementos Libros V-IX. Hemos seleccionado literatura similar en nombre y significado con la esperanza de proporcionar lectores con más opciones para encontrar obras nuevas, interesantes y aún no leídas.
Discusión, reseñas del libro Elementos Libros V-IX y solo las opiniones de los lectores. Deja tus comentarios, escribe lo que piensas sobre la obra, su significado o los personajes principales. Especifica exactamente lo que te gustó y lo que no te gustó, y por qué crees que sí.













