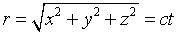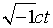Apéndice
1
Una derivación sencilla de la transformación de Lorentz
(Anexo a 11)
Con la orientación relativa de los sistemas de coordenadas indicada en la Fig. 2, los ejes de abscisas de los dos sistemas coinciden constantemente. Aquí podemos desglosar el problema y considerar primero únicamente sucesos que estén localizados en el eje de las X. Un suceso semejante viene dado, respecto al sistema de coordenadas K, por la abscisa x y el tiempo t, y respecto a K' por la abscisa x' y el tiempo t'. Se trata de hallar x' y t' cuando se conocen x y t.
Una señal luminosa que avanza a lo largo del ejeX positivo se propaga según la ecuación
x = ct
o bien
x – ct =0 [1]
Dado que la misma señal luminosa debe propagarse, también respecto a K', con la velocidad c, la propagación respecto a K' vendrá descrita por la fórmula análoga
x’ – ct’ =0 [2]
Aquellos puntos del espacio-tiempo (sucesos) que cumplen (1) tienen que cumplir también (2), lo cual será el caso cuando se cumpla en general la relación
x’ – ct’ = λ (x – ct) [3]
donde λ es una constante; pues, según (3), la anulación de x - ct conlleva la de x'-ct'.
Un razonamiento totalmente análogo, aplicado a rayos de luz que se propaguen a lo largo del ejeX negativo, proporciona la condición.
x’ + ct’ = μ (x + ct) [4]
Si se suman y restan, respectivamente, las ecuaciones (3) y (4), introduciendo por razones de comodidad las constantes
α = (λ + μ) / 2
β = (λ - μ) / 2
en lugar de las constantes λ y μ, se obtiene [5]
x’ = ax – bct
ct’ = act - bx
Con ello quedaría resuelto el problema, siempre que conozcamos las constantes a y b; éstas resultan de las siguientes consideraciones.
Para el origen de K' se cumple constantemente x' = 0 de manera que, por la primera de las ecuaciones (5):
x = bct/a
Por tanto, si llamamos v a la velocidad con que se mueve el origen de K' respecto a K, tenemos que
v = bc/a [6]
El mismo valor de v se obtiene a partir de (5), al calcular la velocidad de otro punto de K' respecto a K o la velocidad (dirigida hacia el ejeX negativo) de un punto K, respecto a K'. Por tanto, es posible decir en resumen que v es la velocidad relativa de ambos sistemas.
Además, por el principio de la relatividad, está claro que la longitud, juzgada desde K, de una regla de medir unitaria que se halla en reposo respecto a K' tiene que ser exactamente la misma que la longitud, juzgada desde K', de una regla unidad que se halla en reposo respecto a K. Para ver qué aspecto tienen los puntos del eje X' vistos desde K basta con tomar una «fotografía instantánea» de K' desde K; lo cual significa dar a t (tiempo de K) un valor determinado, p. ej. t = 0.
De la primera de las ecuaciones (5) se obtiene:
x' =ax.
Así pues, dos puntos del eje X' que medidos en K' distan entre sí x' = 1, tienen en nuestra instantánea la separación:
Δx = 1/a [7]
Pero si se toma la fotografía desde K' (t' = 0), se obtiene a partir de (5), por eliminación de t y teniendo en cuenta (6):
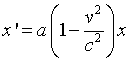
De aquí se deduce que dos puntos del ejeX que distan 1 (respecto a K) tienen en nuestra instantánea la separación
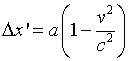 [7a]
[7a]
Teniendo en cuenta que, por lo que llevamos dicho, las dos fotografías deben ser iguales, x en (7) tiene que ser igual a x' en (7a), de modo que se obtiene:
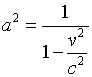 [7b]
[7b]
Las ecuaciones (6) y (7b) determinan las constantes a y b. Sustituyendo en (5) se obtienen las ecuaciones cuarta y quinta de las que dimos en el epígrafe 11.
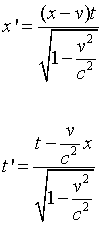 [8]
[8]
Con ello hemos obtenido la transformación de Lorentz para sucesos localizados en el eje X; dicha transformación satisface la condición
x’2 – c2t’2 = x2 – c2t2 [8a]
La extensión de este resultado a sucesos que ocurren fuera del eje X se obtiene reteniendo las ecuaciones (8) y añadiendo las relaciones
y’ = y
z’ = z [9]
Veamos ahora que con ello se satisface el postulado de la constancia de la velocidad de la luz para rayos luminosos de dirección arbitraria, tanto para el sistema K como también para el K'.
Supongamos que en el instante t = 0 se emite una señal luminosa desde el origen de K. Su propagación obedece a la ecuación:
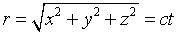
o bien, elevando al cuadrado
x2 + y2 + z2 – c2t2 = 0 [10]
La ley de propagación de la luz, en conjunción con el postulado de la relatividad, exige que la propagación de esa misma señal, pero juzgada desde K', ocurra según la fórmula correspondiente
r' = ct'
o bien
x’2 + y’2 + z’2 – c’2t’2 = 0 [10a]
Para que la ecuación (10a) sea una consecuencia de (10), tiene que cumplirse que:
x’2 + y’2 + z’2 – c’2t’2 = σ(x2 + y2 + z2 – c2t2) [11]
Puesto que la ecuación (8a) tiene que cumplirse para los puntos situados sobre el eje X, ha de ser σ = 1. Es fácil ver que la transformación de Lorentz cumple realmente la ecuación (11) con σ = 1, pues (11) es una consecuencia de (8a) y (9), y por tanto también de (8) y (9). Con ello queda derivada la transformación de Lorentz.
Es preciso ahora generalizar esta transformación de Lorentz, representada por (8) y (9).
Evidentemente es inesencial que los ejes de K' se elijan espacialmente paralelos a los de K. Tampoco es esencial que la velocidad de traslación de K' respecto a K tenga la dirección del eje X. La transformación de Lorentz, en este sentido general, cabe desglosarla —como muestra un simple razonamiento— en dos transformaciones, a saber: transformaciones de Lorentz en sentido especial y transformaciones puramente espaciales que equivalen a la sustitución del sistema de coordenadas rectangulares por otro con ejes dirigidos en direcciones distintas.
Matemáticamente se puede caracterizar la transformación de Lorentz generalizada de la siguiente manera: Dicha transformación expresa x', y', z', t' mediante unas funciones homogéneas y lineales de x, y, z, t que hacen que la relación
x’2 + y’2 + z’2 – c’2t’2 = x2 + y2 + z2 – c2t2 [11a]
se cumpla idénticamente. Lo cual quiere decir: si se sustituye a la izquierda x', etc.
por sus expresiones en x, y, z, t, entonces el miembro izquierdo de (11a) es igual al derecho.
2
El mundo cuadridimensional de Minkowski
(Anexo a 17)
La transformación de Lorentz generalizada puede caracterizarse de un modo aún más sencillo si en lugar de t se introduce como variable temporal la variable imaginaria
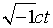
















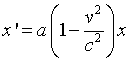
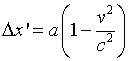 [7a]
[7a]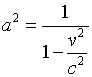 [7b]
[7b]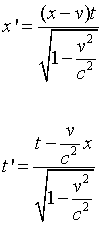 [8]
[8]