Frank J. Swetz
Prefacio
Durante años he trabajado con profesores y estudiantes fomentando la inclusión de material histórico en la enseñanza de las matemáticas; un material que ayuda a humanizarlas, pues las asocia a sus raíces humanas y responde a preguntas como: ¿por qué aparecieron las matemáticas? ¿Cómo se utilizaban? ¿Por qué son importantes? Una información que los estudiantes necesitan para poder responder a las eternas dudas que los acosan: ¿esto para qué sirve? ¿Acaso lo vamos a utilizar alguna vez? En unos currícula ya de por sí atiborrados, la introducción de nuevos materiales resulta complicada; pero he descubierto que un modo eficiente, fructífero y atractivo de incorporar contenido histórico a las matemáticas es mediante el uso de problemas reales propuestos y resueltos por nuestros antepasados. Un sistema del que, en charlas y actividades profesionales relacionadas con este tema, los profesores que lo apoyan me han comentado sus impresiones.
En un libro de actividades pensado como herramienta de enseñanza en clase de matemáticas, Learning activities from the history of mathematics (Swetz, 1994), incluí una sección sobre problemas matemáticos. Problemas que fueron recibidos con entusiasmo por los lectores, quienes los utilizaron con éxito con sus estudiantes. Posteriormente, como editor de la revista electrónica Loci , publicada por la Mathematical Association of America, se me ocurrió compilar la sección «Problems from another time» («Problemas de otros tiempos»), que ofrecía una amplia selección de problemas históricos para ser utilizados en las aulas. Los profesores volvieron a apreciar mi esfuerzo, comprobando que su contenido motivaba mucho a los alumnos, tanto durante las clases como a la hora de hacer los deberes.
Animado por esta respuesta, y siendo de la firme opinión de que tales problemas son un valioso recurso didáctico, he dedicado este libro a la cuestión del uso de problemas históricos en la enseñanza de las matemáticas. Los materiales que en él se incluyen pretenden ser especialmente adecuados para las necesidades de los profesores y alumnos de matemáticas de secundaria; pero considerar estos problemas y sus implicaciones también resultará beneficioso para aquellos universitarios que estudien matemáticas generales o historia de las matemáticas. Los primeros dos capítulos permiten obtener una visión general sobre la relevancia de los problemas históricos tanto en el proceso de aprendizaje como en la comprensión de las matemáticas, además de presentar diversas estrategias para el uso de los mismos. A continuación, los capítulos del 3 al 16 proporcionan una selección de aproximadamente quinientos problemas. El capítulo 17 presenta las soluciones técnicas que con mayor probabilidad fueron utilizadas en la época en la que se concibieron los problemas, es decir, los métodos utilizados por quienes primero los resolvieron. Por último, en el capítulo 18 hablo sobre el uso de los problemas históricos y animo al lector a buscar otros.
Los problemas se han seleccionado atendiendo tanto a su adecuado contenido matemático como a las diferentes historias sociales y culturales que nos cuentan sobre los usos de las matemáticas. Sus orígenes van desde las inscripciones cuneiformes en antiguas tablillas babilónicas del 2000 a. C. hasta el Papiro matemático Rhind egipcio (1650 a. C.), pasando por el manual matemático chino Los nueve capítulos (c. 100 d. C.); desde el primer libro impreso en Europa sobre aritmética, la Aritmética de Treviso (1478), hasta The Ladies Diary del siglo xviii y el Farmer’s Almanac del siglo xix del Salvaje Oeste. Cada serie de problemas viene precedida por un prefacio con algunos comentarios pertinentes y algunas ilustraciones escogidas.
Analizar y estudiar estos problemas puede servir para presentar a la clase un nuevo concepto matemático o reforzar alguno ya estudiado. En sí mismo, cada problema también proporciona una breve anécdota sobre por qué se necesitan las matemáticas. Igualmente, el contexto de los problemas proporciona al lector detalles sobre cómo era la vida de las personas en la época en la cual fueron escritos. Su contenido conecta las matemáticas con la sociedad y, dado que no son elementos cerrados, este aspecto permite utilizarlos tanto para la enseñanza interdisciplinar como para generar diferentes debates en clase.
Como complemento a los distintos grupos de problemas hay breves digresiones tituladas «¿Qué están haciendo?». Su objetivo es enriquecer aún más la comprensión de los problemas matemáticos llegados de épocas lejanas, pues destacan algunos de los interesantes rasgos culturales e históricos que se encuentran en ellos y proporcionan pistas sobre el proceso seguido antaño para su resolución. Las soluciones a los problemas se encontrarán al final del libro, junto a un glosario de términos y una bibliografía que incluye tanto sugerencias de lectura, como las fuentes citadas en el texto.
Mi esperanza es que los profesores experimenten con las ideas y conceptos aquí presentados, que se embarquen en expediciones de aprendizaje y comprensión junto con sus estudiantes y que terminen creando sus propias colecciones de problemas históricos, gracias a los cuales tanto ellos como sus alumnos pueden acabar apreciando aún más las matemáticas y sus orígenes humanos.

Los problemas matemáticos
1. Los problemas descriptivos. Huellas de la historia de las matemáticas
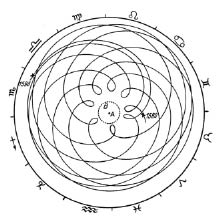
Dibujo de la órbita de Marte realizado por Johannes Kepler y publicado en su Astronomia nova (1609). Muestra el aparente movimiento retrógrado del planeta tal cual fue registrado entre 1580 y 1596 siguiendo la por entonces imperante teoría ptolemaica. En su época, este diagrama era llamado panis quadragesimalis , o «pan de Cuaresma». Utilizando los precisos datos que acumuló durante quince años de observaciones astronómicas, Kepler refutó esa teoría y demostró que el planeta recorría una órbita elíptica.
Una visión general
Desde un punto de vista histórico, resulta interesante, así como bastante revelador, que algunos de los primeros textos escritos consistan en «problemas descriptivos». Estos ejercicios para el aprendizaje de las matemáticas tienen miles de años de antigüedad y aparecieron por primera vez en la cuenca del Tigris-Éufrates, la antigua Mesopotamia. Los millares de tablillas de arcilla descubiertos por los arqueólogos en esta región permiten entrever la evolución de la escritura. Las tablillas más antiguas que se han encontrado presentan la huella de diferentes fichas de barro, contadores matemáticos concretos cuya marca impresa designaba un valor numérico. Poco a poco, este sistema se fue incorporando a una forma más flexible de escritura, la cuneiforme.
Parece que los primeros productos de este proceso fueron tabillas numéricas, registros que contenían datos de actividades sociales como las cantidades recogidas durante la cosecha o los impuestos pagados y «textos con problemas», es decir, conjuntos de problemas para los que se buscaba una solución, o bien un problema concreto con una respuesta y el proceso que conducía a su solución. La excavación en el recinto de un templo de la ciudad sumeria de Shuruppog sacó a la luz el más antiguo de los problemas descriptivos conocidos, redactado durante el iv milenio a. C.
















