Angélica Chappe - Introducción a las matemáticas

© Institución Universitaria Politécnico Grancolombiano Introducción a las Matemáticas

Autores:

Angélica Chappe

Martha Zambrano

Diego Arévalo

ISBN: 978-958-8721-13-2

E ISBN: 978-958-8721-14-9

Editorial Politécnico Grancolombiano

Calle 57 No. 3-00 Este Bloque A Primer piso

PBX: 7455555 ext. 1170

www.poligran.edu.co/editorial

Noviembre de 2012

Bogotá, Colombia

ePub x Hipertexto Ltda. / www.hipertexto.com.co

Institución Universitaria Politécnico Grancolombiano

Facultad de Ingeniería y Ciencias Básicas

Fernando Dávila Ladrón de Guevara

Rector

Rafael García

Decano Facultad de Ingeniería y Ciencias Básicas

Eduardo Norman Acevedo

Director editorial

David Ricciulli

Coordinador editorial

Nydia Patricia Gutiérrez

Corrección de estilo

Leonardo López

Diseño y armada electrónica

Juan Gómez

Fotografía portada

La Editorial del Politécnico Grancolombiano pertenece a la Asociación de Editoriales Universitarias de Colombia, ASEUC.

El contenido de esta publicación se puede citar o reproducir con propósitos académicos siempre y cuando se dé cuenta de la

fuente o procedencia. Las opiniones expresadas son responsabilidad exclusiva del autor.

Capítulo 1

Se tienen 12 monedas iguales en apariencia, pero una de ellas pesa distinto que el resto. Con todo, no se sabe si pesa más o menos, solo que pesa diferente. El objetivo es descubrirla. Para ello, se cuenta con una balanza de dos platillos. En realidad, es una balanza muy sencilla que solo detecta si lo que se pone en uno de los platillos pesa más, igual o menos que lo depositado en el otro. Nada más. Para descubrir la moneda distinta se pueden efectuar solo tres pesadas, ¿cómo encontrar la moneda del peso diferente?

Problema presentado en el libro “ Matemática, ... ¿Estás ahí?” de Adrián Paenza [3]

Dentro del desarrollo de nuestras actividades diarias, en algunas ocasiones es necesario conocer la cantidad de objetos de un conjunto. Por ejemplo, ¿cuántas canciones puedo almacenar en mi reproductor de música? ¿cuántos amigos están conectados? ¿cuántas horas faltan para salir del trabajo? ¿cuántos días hacen falta para mi cumpleaños? ¿cuántos estudiantes conozco en la clase de matemáticas?

Ejercicio 1. Cite un ejemplo de una situación cotidiana, donde sea necesario contar.

Para dar respuesta a cada uno de los interrogantes anteriores, empleamos números como 2, 5, 7, 11, etc. que pertenecen al conjunto de los números naturales (N).

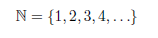
Ejercicio 2. ¿Qué representan los puntos suspensivos en la línea anterior?

Parte 1: Trabajando con los números naturales

Antes de iniciar “las cuentas”, es indispensable detenerse en el concepto: termino de una expresión algebraica , en particular, de una expresion aritmetica. La idea en este punto es, identificar cuales son los terminos en una expresión.

En el conjunto de los números naturales están definidas las operaciones: adición y multiplicación, y sobre éstas, algunas propiedades. Antes de presentarlas formalmente, se hará una primera aproximación a ellas.

Ejercicio 3. En cada una de las siguientes expresiones algebraicas, indique cuántos términos hay y señálelos (no efectúe operaciones):

Ejercicio 4- Retome el ejercicio anterior y ahora sí, efectúe las operaciones indicadas (no emplee calculadora).

Aunque los números naturales permiten responder a situaciones de conteo, otros escenarios exigen representaciones distintas, específicamente, aquellas en donde se requiere un punto de referencia (el número cero) y otros números “contrarios” a los naturales. Esto exige disponer de un nuevo conjunto: el de los números enteros.

Parte 2: Un nuevo conjunto

Lea detenidamente las siguientes frases:

• La temperatura en un refrigerador es de tres grados bajo cero.
• La empresa XYZ presenta este mes en su balance, perdidas por $20.000.000.
• Súcrates naciú en el año 470 a.C.
• El señor Alberto adquiriú una deuda de $5.000.000.

Al tratar de representar mediante nuúmeros naturales las afirmaciones anteriores, aparecen algunas limitaciones de este conjunto que se resolverán haciendo una “extensiún” al sistema de los naturales.

Sobre la siguiente recta numúerica se representan los nuúmeros naturales y el cero:

Ahora, para cada número natural n se construye un punto localizado a la izquierda del origen y que esté a la misma distancia de 0 que n. A este punto se denota como — n y se hará referencia a él como el opuesto de n.

Por ejemplo, sea n = 3, entonces el opuesto de 3, el cual denotamos por —3, está representado por el punto localizado tres unidades a la izquierda de 0.

Aunque la noción de opuesto se construye para números naturales, esta definición se puede emplear de un modo más general y así cuestionarse por la ubicación del opuesto, por ejemplo, de —7. De acuerdo con lo expuesto, el número localizado a la derecha de cero que esté a la misma distancia de 0 que —7 es el número 7, es decir, el opuesto de —7 es 7.

Ejercicio 5. Indique y localice el opuesto de —3 y 5.

Parte 3 : Propiedades de la operaciones

El conjunto de números conformado por los números naturales, sus opuestos y el cero es denominado el conjunto de los números enteros y se describe como Z = {..., —3, —2, —1, 0, 1, 2, 3,...}

Como en el caso de los números naturales, en el conjunto de los números enteros están definidas las operaciones de adición y multiplicación; algunas de sus propiedades se presentan a continuación.

Sean a, b y c números enteros:

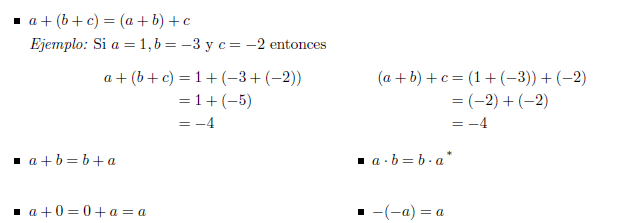
* En la literatura, se representa la multiplicación entre los números a y b por la expresión a • b, ab , (a)(b) o a(b).