Mariano Mataix Lorda - Dúo matemático

MARIANO MATAIX LORDA

SUSANA MATAIX HIDALGO

Dúo matemático

© de los autores, 1995

Escaneado: Jacgarper

Edición digital: Sargont (2019)

ISBN: 84-267-1005-0

Depósito Legal: B-5922-1995

Impreso en España

Printed in Spain

Este libro es el resultado de una colaboración que siempre existió de una forma más o menos esporádica, aunque sólo se plasmó anteriormente en labor crítica de una de las partes. Creemos llegado el momento de que la aportación no sea sólo crítica, sino también creativa, y que la que criticó sea también criticada. Que el dúo funcione y sepa cumplir con su raigambre matemática alcoyana, solamente el público ―único juez válido― puede decirlo. Confiamos en que su juicio nos sea favorable.

A don Félix de Montemar su padre le dejó por herencia un terreno de forma rectangular y 12 hectáreas de superficie. Consultaba a Arquímedes García cómo podría dividirlo, sin saber las dimensiones, de forma que pudiese ofrecer a un ocasional comprador una parcela de cualquier superficie que fuese un número entero de hectáreas igual o menor que doce.

Arquímedes García le dijo que ello podía hacerse levantando dos vallas rectas en el terreno, con tal de que fuese posible eliminar trozos de valla entre terrenos contiguos para formar parcelas mayores. Parcelas que no tengan valla común no pueden reunirse; y al decir que se puedan retirar trozos de valla entre terrenos colindantes debemos entender que dichos terrenos se juntan totalmente.

¿Será usted capaz de emular a Arquímedes García?

Un aficionado al fútbol del año 2000 leía una crónica del pasado en la que se explicaba que en cierta ocasión el Madrid eligió su presidente entre cuatro candidatos: Bemabeu, De Carlos, Mendoza y Ussía. Cada uno de los cuatro debió elegir, antes de la votación, a su candidato preferido de entre los otros tres, pero sin permitirse componendas de «yo te elijo a ti y tú a mí», lo que traducido quiere decir que no pueden darse preferencias recíprocas como, por ejemplo: Bemabeu eligió a Mendoza y Mendoza a Bemabeu. Esta elección de preferido implicaba que caso de ser eliminado un candidato, sus votos pasaban a su preferido en la votación siguiente. La regla para la votación era que el que menos votos sacaba era eliminado, e igualmente quedaba eliminado un candidato si su preferido sacaba más votos que él. Aclarándolo con un ejemplo, supongamos que Bemabeu eligió a Mendoza. Se produce una votación y en ella sale último De Carlos y Mendoza saca más votos que Bemabeu. De Carlos -por quedar último- es eliminado; e igualmente Bemabeu por haber sacado menos votos que Mendoza. Y ello aunque Mendoza hubiese quedado eliminado por haber sacado menos votos que su preferido. Además, los votos de Bemabeu irían a Mendoza en la votación siguiente, e igualmente irían los de De Carlos a su preferido. Como vemos, la elección está un poco complicada, pero eso es lo bueno.

Así, en cada elección se eliminó al menos uno de los cuatro. Los que quedaron procedieron a una nueva votación. En el caso que leía quien se aproximaba al comienzo del siglo veintiuno, dos candidatos pasaron a la segunda elección. Ussía obtuvo los mismos votos en ambas. ¿Cuál fue el orden de candidatos (por número de votos) en la primera votación? ¿Quién ganó finalmente en la segunda?

Se me olvidaba: Bemabeu eligió a Ussía, mientras Mendoza fue el elegido de Ussía y De Carlos.

Advertencia: Los electores eran consecuentes y votaban siempre de la misma manera, con la sola alteración de la norma implicada en las preferencias.

El siguiente problema me fue remitido por el Dr. Hayo Ahlburg.

En una reunión de amigos, Matilde dice: «Yo he mentido solamente tres veces en mi vida». A lo que contesta el Sr. Sánchez: «Entonces ésta ha sido su cuarta mentira».

¿Es cierto o no lo que dice el Sr. Sánchez?

En una cena que compartía con el matemático suizo Samuel Koenig, éste hizo alarde de haber resuelto con gran trabajo un difícil problema. Bernoulli continuó disfrutando de la cena, y cuando pasaron al café ofreció a Koenig otra solución más elegante del problema.

Como siempre, las cifras han sido sustituidas por letras.

Otro de los famosos rompecabezas de Sam Loyd es éste que vemos en la figura. Las seis piezas pueden disponerse de forma que se obtenga un caballo al trote.

Actualmente, el fallo de los jóvenes en los exámenes de matemáticas resulta preocupante. Tal vez influya el que no recurran a tantos versos y canciones como anteriormente, lo que era una buena ayuda para los estudiantes. Mi amigo Aurelio González-Isla me informa del siguiente verso, medio esproncediano, medio matemático, para recordar el teorema de Rolle.

Las ilusiones perdidas

juguete del viento son.

Las variaciones perdidas

raíces son, ¡ay!, desprendidas

del árbol de la ecuación.

El teorema de Rolle decía ―y sigue diciendo― que entre dos raíces consecutivas de una ecuación hay por lo menos una, y en general un número impar, de la ecuación derivada. Por consiguiente, el vate debe llamar raíces desprendidas del árbol de la ecuación, a las raíces de su derivada. Y es claro que en las raíces de la derivada la tangente de la función es horizontal y la variación «se pierde», o lo que es lo mismo, es cero o no existente.

Así se designan ciertas curvas cuyo comportamiento resulta inusual, entre las cuales el copo de nieve de Koch es una de las más conocidas, de gran interés actualmente en el estudio de las configuraciones fractales, según la denominación de Benoit Mandelbrot, uno de los adelantados en él estudio de las configuraciones que se repiten a escala diferente en una misma imagen. Veamos la curva de Koch.

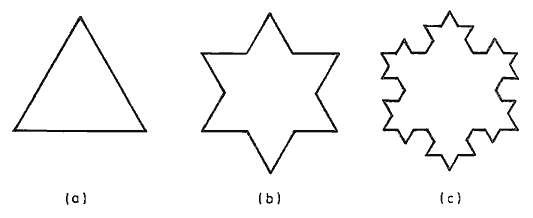
Tracemos un triángulo equilátero de lado igual a 1. Su perímetro vale 3. Dividamos cada lado en tres partes iguales y en la central levantemos otro triángulo equilátero de lado 1/3, tal como indica la figura (b). El perímetro vale ahora 3 × 4/3, y el área encerrada por la curva habrá aumentado en la de los tres pequeños triángulos.