Mariano Mataix - Cajón de sastre matemático

MARIANO MATAIX LORDA

Cajón de sastre

matemático

© M. Mataix, 1993

Escaneado: Jacgarper

Edición digital: Sargont

ISBN: 84-267-0221-X

Depósito Legal: B. 1519-1993

Impreso en España

Printed in Spain

En el original, la solución está en la misma página del problema.

La he trasladado a la página siguiente para mejorar la legibilidad.

A Petárdibus, que debía haber compartido

la elaboración de este libro, y no lo ha hecho.

El presente libro, al que he llamado «Cajón de sastre matemático» tratando de reflejar lo más claramente posible su contenido, es un revoltijo de problemas y curiosidades matemáticas, que espero entretengan e interesen al lector como a mí me interesaron y entretuvieron. De todo hay en él y si, al final, el lector llega a la conclusión de que las matemáticas pueden ser amenas y divertidas, su fin estará conseguido.

E L AUTOR

Uno de nuestros más famosos humoristas, Wenceslao Fernández Flórez, resolvió, en tiempos de falta de tabaco, como ocurrió durante la Guerra Civil Española, la forma de fumar tres cigarrillos disponiendo tan sólo de 6 colillas, en el entendido de que son necesarias 3 colillas para hacer un cigarrillo.

Con tres colillas se hace un cigarrillo que, al final, da una colilla, que unida a las tres que nos sobraban hace un total de cuatro.

Empleamos otras tres en el segundo cigarrillo recuperando una colilla, que unida a la que nos había sobrado da un total de dos.

¿Cómo, entonces, podremos fumar ese tercer cigarrillo?

Muy fácil. Le pedimos prestada una colilla a un amigo, lo que nos permite, con las otras dos, hacer el cigarrillo y, una vez terminado éste, le devolvemos la colilla al amigo.

Una persona coloca 1 peseta en el banco al interés del 100%. Al final del año, el capital será de 2 pesetas. (Capital inicial + intereses.)

Pero considera que el interés compuesto debe ser, no anual, sino semestral y que, por tanto, el banco ha de darle el 100/2% semestral. En este caso, al cabo del año la peseta se habrá convertido en

c (1 + i ) = 1 × (1 + ½) = 2,25 ptas.

Siguiendo en la misma línea, quiere ahora que sea mensual, con lo que el interés es 100/12, y la peseta se habrá transformado, al cabo de un año, en

1 × (1 + 1/12) = 2,61 ptas.

Finalmente, querría que el interés fuese continuo. En tal caso —como vemos, cada vez ha de pagar más el banco— ¿en cuánto se habría convertido la peseta al fin del año? ¿Podría el banco hacer frente al desembolso?

Sí podrá hacer frente el banco al desembolso, ya que será

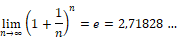
Gracias a los triunfos de Santana y Orantes el deporte del tenis ha tomado un gran auge. No hay club que no organice su torneo y los organizadores deben calcular el número de partidos que se han de jugar para llegar a proclamar el campeón, a fin de hacer un acertado plan de utilización de las pistas.

Cuando los inscritos son un número que es potencia de dos, digamos, por ejemplo, 32, es fácil ver que en la primera ronda se jugarán 16 partidos, 8 en la segunda, 4 en la tercera, etc., y llegar así al resultado final del número de partidos que han de jugarse. Pero, ¿cuántos partidos habrán de jugarse si los inscritos son 67?

Este problema es un ejemplo claro de cómo la solución puede ser inmediata con un buen planteamiento. Para ello sólo es preciso tener en cuenta que en cada partido se elimina un concursante y, puesto que hay un ganador, 66 habrán de eliminarse. Igual número, por tanto, de partidos a jugar.

El problema siguiente es un caso típico de definición poco precisa y tiene, a mi entender, una importante moraleja didáctica. Más que nunca hoy día, en que tan frecuente resulta el oír expresar a algunos profesores su indignación por la incompetencia de los alumnos que han sido incapaces de resolver un problema tan sencillo como el que habían puesto en examen... Sin que nunca se paren a pensar que ese problema tan sencillo, si casi todos los alumnos lo han fallado, teniendo en cuenta que biológicamente la humanidad progresa, es muy posible que esté, sencillamente, mal definido. Esto es, ellos han pensado una cosa y creído que en el enunciado la expresaban, pero no era así. Y con ello vamos a nuestro problema. Lo he sacado de un libro bien conocido y se expresaba como sigue:

¿Cuántas ovejas saltan una valla, en una hora, si diez saltan la valla en 10 minutos?

Naturalmente, la contestación evidente —y que por ello no ha de ser la correcta para el autor— es 60 ovejas.

El autor explica que no es así, sino 55. Dice: Si 10 ovejas saltan la valla en 10 minutos —midiéndose el tiempo desde el salto de la primera hasta el salto de la décima— el intervalo entre saltos es 10/9 minutos: Hay 60/(10/9) de tales intervalos en una hora, de modo que son 55 las ovejas que la saltan en este tiempo.

La clave de la solución está en la frase indicada en letra cursiva (por nosotros, no por el autor). Cuando enunció el problema no dijo cómo se cronometraban las ovejas, y después le parece que es forzoso pensar que se hizo poniendo en marcha el cronómetro al saltar la primera (y contándola), para pararlo al saltar la décima (y contarla también). Pero un cronometrador más lógico, si ponía en marcha el cronómetro al saltar una oveja y lo paraba al saltar otra, no contaría la primera si tenía en cuenta la segunda. Este cronometrador diría que habían saltado 9 ovejas en 10 minutos. Luego, en 60 minutos, saltarán 54.

Otra forma de cronometrar, diferente y más lógica de la supuesta por el autor, sería poniendo en marcha el cronómetro en un momento cualquiera, que lógicamente no coincidiría con un salto, y contando el número de saltos en 10 minutos. Aquí, 10 saltos en 10 minutos corresponderían a un salto por minuto y la solución sería 60.

Finalmente, aun con su forma de cronometrar, introduce una segunda arbitrariedad, en cierto modo consecuente con la primera, que es la de dar como resultado 55 en vez de 54, lo que supone que la medida para una hora se hace también empezando con el salto de una oveja en el instante cero, la cual se contabiliza, y terminando, claro está, con otro salto, que también se contabiliza, lo que es ilógico, ya que, aún suponiendo el salto de duración casi nula, habrá que considerar instantes análogos, es decir, la oveja comenzando o finalizando el salto en ambos casos. Dicho de otro modo, la oveja siempre contada a un mismo lado de la valla.

Me he extendido sobre problema tan sencillo para insistir en lo que queda dicho al comienzo. Cuando un profesor pone un problema que cree fácil y la mayoría de la clase lo hace mal, lo primero que debe pensar es que quizá no sea tan fácil como creía; probablemente por estar mal definido. Pero pensar que, repentinamente, todos sus alumnos se han vuelto tontos o confabulado para no estudiar, es pura insensatez.

Cinco por cuatro veinte, más dos, igual a veintitrés. ¿Es cierto o falso?

Es tan sólo una cuestión de lenguaje:

5 × 4,20 + 2 = 23.

Supongamos que está Ud. casado (o casada) y lleva un anillo. Cojamos un hilo y rodeemos el anillo con él, cortándolo de forma que dé justo para rodearle una vez. La longitud de este hilo será de unos 6 cm.

Empalmémosle ahora 6 m más de hilo, esto es, cien veces su longitud. Si lo disponemos formando un círculo, este círculo quedará muy holgado. De hecho, quedará con una separación de 1 m entre él y el círculo concéntrico del anillo.