Mariano Mataix - Ocio Matemático

MARIANO MATAIX LORDA

Ocio

matemático

© M. MATAIX LORDA, 1984

Escaneado: Jacgarper

Edición digital: Sargont (2019)

ISBN: 84-267-0549-9

Depósito legal: B. 21.189 – 1984

Impreso en España

Printed in Spain

En recuerdo de Juan Jesús Torán y la entrañable amistad de toda una vida.

En el hipódromo de la Zarzuela no hubo más que tres caballos en una carrera: Dinamita, Boyardo y Estrella Dorada. Las apuestas eran de 9 a 1 contra Dinamita, y de 3 a 2 a favor de Boyardo. ¿Cómo estaban —o debían estar, ya que a veces los apostantes no actúan de acuerdo con las matemáticas— las apuestas para Estrella Dorada?

En cierta ocasión un hijo le decía a su padre:

— Papá, hoy no voy a ir al colegio; te daré tres razones para ello: La primera, que tengo sueño; la segunda, que me aburro; la tercera, que los niños se ríen de mí.

A lo que el padre le contestó:

— Pues yo te daré otras tres para que vayas: La primera, que es tarde; la segunda, que tienes 45 años; y la tercera, que eres el director del colegio.

* * *

Si el lector tiene un concepto de la lógica tan claro como el del padre, no le será difícil el siguiente problema:

En el parlamento de Carabia están representados solamente tres partidos políticos: el tradicional, el hiperácrata y el ecléctico. Los miembros del partido tradicional se aferran a la tradición caballeresca de no mentir jamás. Por oposición, como no podía menos de suceder, los hiperácratas, para marcar su total enfrentamiento con los tradicionales, mienten siempre. Finalmente, los eclécticos unas veces mienten y otras no.

Al entrar en el parlamento encontré a tres diputados que discutían en forma tal que no cabía duda de que cada uno pertenecía a un partido político diferente. Al preguntarles sobre sus respectivas filiaciones

el primero dijo: soy ecléctico

el segundo: ello es cierto

el tercero: no soy ecléctico

¿Cuál era el partido de cada uno?

En el parlamento de Dualia sólo hay tradicionales e hiperácratas (véase el problema anterior). El otro día me presentaron al Presidente del Congreso y al del Senado. Quise saber a qué partido pertenecía cada uno, y el Presidente del Consejo me contestó: “Al menos uno de nosotros es un hiperácrata”. ¿Qué es cada uno?

Latinia es un país que formaba parte de Dualia —donde sólo había tradicionales e hiperácratas— y actualmente es independiente. Como resultado en su parlamento hay dos partidos: azul y rojo. En cada uno de estos partidos, los diputados provenían de los tradicionales e hiperácratas de Dualia, y han continuado con sus respectivas costumbres de ser veraces y mendaces, respectivamente. Así, en el parlamento de Latinia los diputados de cada uno de los partidos pueden ser procedentes de tradicionales e hiperácratas, dando lugar a cuatro tipos diferentes: azul-tradicional, azul-hiperácrata, rojo-tradicional y rojo-hiperácrata. Dos de ellos veraces, y dos mendaces.

Al preguntarle a un diputado qué era, me contestó: “Soy un rojo-hiperácrata”. ¿Qué era?

Gabriel y Galán, el cantor de las tierras de Extremadura, plantea el siguiente problema aritmético en una de sus “Extremeñas”, la que lleva por título “Varón”:

“Sácame la cuenta

del aceiti que hogañu nos toca

del lagal pol la partí que es nuestra.

Se maquilan sesenta cuartillus

pa ca parti entera,

y nosotros tenemus, ya sabis,

una media tercia,

que tu madre hereó de una quinta

que tenía tu agüela Teresa”

Como vemos está escrita en el dialecto extremeño, lo que le da mayor actualidad. ¿Cuál es su solución?

Un agricultor tenía una finca cuadrada de 1 km de lado. Ofreció a un amigo vendérsela toda o parte de ella, sin cargarle nada por el terreno, provisto que le dejase vallarla a 200 ptas. por metro. Caso de comprar solamente una parte, el comprador podía elegir el terreno en la forma que quisiere, y así lo hizo, buscando comprar el mayor terreno posible con tal de que el precio por metro cuadrado fuese el mínimo. ¿Qué terreno compró?

Sobre el polo Norte de una esfera terrestre colocamos una bolita de acero. Al soltarla comenzará a descender y se separará de la esfera, cayendo al suelo. ¿En qué latitud se producirá la separación de la bolita y la esfera?

Un muchacho, jugando con bolas blancas y negras, en número total menor de 1000, se dio cuenta de que podía colocar las blancas en una matriz perfectamente cuadrada, formando las negras una ampliación de la matriz cuadrada, al colocarlas exteriormente. Por otra parte, con las negras podía a su vez formar una matriz cuadrada, de un orden superior al de las blancas [es decir, que si por ejemplo las blancas son a, las negras habrán de ser (a + l)], provisto que en el centro colocase una bola blanca para completar la matriz. ¿Cuántas bolas blancas y negras tenía?

Aunque este problema parece idéntico al anterior, no lo es.

Se tiene un tablero cuadriculado, semejante a la matriz de un crucigrama, y un montón de fichas blancas y otro de fichas negras, cuyo número total no sobrepasa 500. Las fichas blancas forman una matriz cuadrada en el centro del tablero. Las negras, puestas alrededor en los cuadrados vacíos, completan el tablero. Por otra parte, las fichas negras forman a su vez una matriz cuadrada en el centro del tablero, de un orden superior al de las blancas, provisto que se coloque una ficha blanca en el centro. ¿Cuál es el número de fichas de cada color?

Esta famosa matemática italiana nació y murió en Milán (16 mayo 1718 a 9 enero 1799). Se distinguió, asimismo, como lingüista y filósofa. Fue profesora de matemáticas en Bolonia, destacando por su trabajo en cálculo diferencial. Era sonámbula, y mientras se hallaba en tal estado, caminaba hasta su estudio y resolvía problemas que la habían dejado perpleja en su estado normal. A la mañana siguiente se sorprendía de encontrar en su mesa, como escrito por otra persona, la solución de los problemas que había dejado sin resolver. Su texto “Instituzioni analítiche ad uso della gioventú italiana”, dedicado a la emperatriz María Teresa, en 1748, incluye una discusión de la curva de Agnesi o curva “versiera”, que debido a una pobre traducción —dado que versiera también significa bruja en italiano— se conoce en inglés como “la bruja de Agnesi”. La curva viene dada por la ecuación: x y = a ( a – y ) y tiene la forma que indica la figura

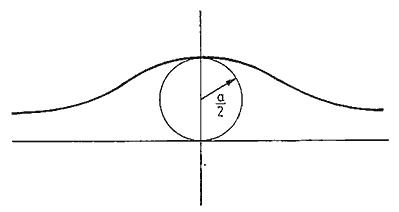
En este tipo de problemas se han hecho tales alardes de ingenio que el siguiente, ideado por Sam Loyd —recordemos que murió en el año 1911— resulta bastante sencillo.