MARIANO MATAIX LORDA
Droga
matemática
© M. MATAIX LORDA, 1983
Escaneado: Jacgarper
Edición digital: Sargont (2019)
ISBN: 84-267-0505-7
Depósito legal: B. 23.022 - 1983
Impreso en España
Printed in Spain
Este libro lo dedico a la memoria de un ser querido que, de vivir, no habría podido leerlo. Porque no era un ser humano; era más que humano.
Y hasta tu recuerdo me lo va secando, esta alma de polvo de los días malos.
(A. Machado)
Índice general
Introducción
Recientemente, en una entrevista para la radio, me preguntaban si creía que las matemáticas podían ser entretenidas, como el título de uno de mis libros, “El discreto encanto de las matemáticas”, parecía sugerir.
Creo, efectivamente, que no solamente pueden ser entretenidas, sino llegar a convertirse en una droga. Pero una droga salutífera o provechosa, a diferencia de las que estamos acostumbrados a oír nombrar en la vida diaria. Lo que no les priva de poder crear drogadicción, siguiendo el mismo camino que es normal en estos casos: droga blanda → droga dura. Ello lo verán reflejado en este libro. La primera parte, droga blanda, no es sino la antesala para la droga dura. Si, al final, salen algunos drogadictos, espero que nadie considere que merezco la cárcel. Vale.
P RIMERA P ARTE
DROGA BLANDA
Enunciados
1. Elecciones y cena
Tras las elecciones generales del mes de Brumario, varios representantes de AP, PC, PSOE y UCD se reunieron en una cena de fraternidad política. El número de los comensales no era muy afortunado: 13 en total. Además se daban las siguientes circunstancias:
1. Los comensales de AP más los del PC sumaban 5.
2. Los comensales de AP más los del PSOE sumaban 6.
3. El número de los comensales de cada partido era diferente.
4. Los comensales del partido ganador en las elecciones eran 2.
¿Qué partido ganó las elecciones de Brumario?
2. El ABC de los criptogramas
ABC = C
BCA = D
3. Dedicatoria
La siguiente dedicatoria, que acompañaba a uno de mis libros enviado a un amigo, constituye un problema que tal vez pueda usted resolver.
“Con sincero sentimiento te dedico este libro en recuerdo de los tiempos del Instituto. Espero que te choque, en el primer momento, lo premioso de mi envío, pero pronto notes que existe un motivo coherente con el contenido mismo del libro, y es que este escrito de remisión, que tiene porte corriente, es en sí mismo un torete que espero detectes y soluciones, diciendo por qué no es un escrito corriente y moliente, como pudiste creer.”
4. Semántica en desuso
En toda lengua existen una serie de palabras que van cayendo en desuso y solamente figuran arrinconadas en los diccionarios, esperando que alguien las retire de la circulación, para hacer sitio a las nuevas que van siendo creadas. En el castellano, y en el tema de matemáticas, he encontrado las siguientes, que seguramente crearán dudas en su definición a los lectores. Haga usted la prueba.
Cuadrivio, potestad, cubocubo, gallarín, aritmómetro
5. El uno y el cien
Escribir el número 1 y el 100 con una expresión —para cada uno— en la que intervengan las 10 cifras, una vez solamente.
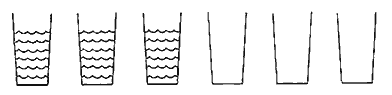
6. Cosas de nuestros tiempos: Alteración del orden
Se trata de conseguir, moviendo un solo vaso, que los vasos vacíos alternen en la fila con los llenos.
7. Abecedario invertido
ABCDE × 4 = EDCBA
Las letras representan las cifras de un número, que al multiplicarle por 4, da el que resulta de invertir el orden de las cifras en el primitivo.
8. Matemática griega
1. ¿Quién fue el primer historiador de las Matemáticas?
2. “Que nadie entre aquí que no sea geómetra.” ¿En qué lugar, según la tradición, se hallaban grabadas estas palabras?
9. La forma más sencilla de instalar un mástil
Un teniente dispone de 1 sargento y 3 soldados para levantar un mástil de 10 m, en el que poner la bandera. El trabajo necesita hacerse antes de 1 hora. Para levantar el mástil hay que hacer una zanja de 1 m de profundidad. Cada soldado es capaz de cavar 10 cm en 10 minutos, y no puede trabajar más de un soldado al mismo tiempo. ¿Cómo solucionaría usted el problema si se hallase en el lugar del teniente?
(A DVERTENCIA : Si no consigue resolver rápidamente este problema, es mejor que no siga esforzándose en ello y vea la solución.)
10. Truco matemático
Diga a uno de los presentes que tome un número cualquiera, compuesto de varias cifras; que altere el orden de éstas y reste el menor del mayor de los dos números (el tomado inicialmente y el resultante de alterar el orden de sus cifras). Finalmente, que elimine una cifra cualquiera del resultado y le diga la suma de las restantes. Seguidamente usted podrá decir cuál fue la cifra borrada; ¿o no podrá? En este segundo caso, vea la solución.
11. Sólo se ven treses
No hay más treses que los que se ven.
12. Filología
Paseando en Madrid, por los alrededores de la Casa de Campo, tropecé con un pedazo de cartel que decía:

Como precisamente iba en compañía de un amigo inglés, traté de que me lo tradujera, pero no pudo hacerlo, seguramente a causa del trozo que faltaba y que se indica en línea de trazos. ¿Puede usted completar el trozo que le falta a la inscripción?
13. Danza eslava
V | A | L | S | E |
S | L | A | V | E |
* | * | * | * | * | * |
* | * | * | * | * | * |
* | * | * | * | * | * |
* | * | * | * | * | * |
* | * | * | * | * | * |
* | * | * | * | * | * | * | L | E |
En este criptograma todas las letras representan números primos.
14. Palíndromos
Un palíndromo es un capicúa, pero con letras. Es decir, “palabra o frase que se lee igual de izquierda a derecha que en sentido inverso”.
En mi infancia, el más conocido fue siempre: “Dábale arroz a la zorra el abad.”
Y uno de los más modernos, nacido de las técnicas que han hecho irrupción con la última guerra mundial: “Radar.”
Otros palíndromos son: “Ananá”, la planta exótica de sabroso fruto; “Alalá”, canto popular del norte de España; y “Yatay”, planta de la familia de las palmas, cuyo palmito es comestible y su fruto se utiliza para fabricar aguardiente.















