V. A. Uspenski - Triangulo de Pascal

PREFACIO

Es imprescindible advertir al lector que no se ha enterado todavía de qué es el triángulo de Pascal, que no se trata de una figura geométrica con tres ángulos y tres lados. Se llama triángulo de Pascal a una importante tabla numérica por medio de la cual se logra resolver toda una serie de problemas de cálculo.

Considerando algunos de ellos, se referirá paso al problema concerniente al significado general de las palabras “resolver el problema”.

La exposición no presupone conocimientos previos cualesquiera que salgan fuera de los límites del programa previsto por la escuela de ocho grados, excepto la definición y designación de la potencia de exponente nulo. Se debe conocer exactamente que todo número distinto de cero, elevado a la potencia cero, se considera (por definición) igual a una unidad: a0 = 1 cuando a 0.

Capítulo 1

PROBLEMA DE LA VIII OLIMPÍADA

En la VIII Olimpíada matemática de Moscú (1945), a sus participantes, alumnos de los grados 9 10, fue prepuesto el siguiente problema:

Se tiene una red de caminos (Figura 1). Desde el punto A parten 21000 hombres. Una mitad de ellos se encaminan en la dirección l, otra, en la m. Al llegar al primer cruce cada grupo se divide: una mitad sigue la dirección l, la otra, la m. Lo mismo ocurre en cada cruce. ¿Cuántos hombres llegarán a todos los cruces de la milésima serie?

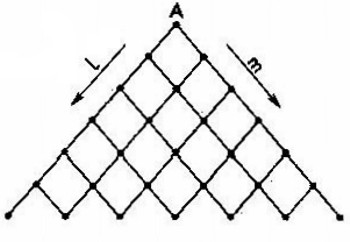
Anunciemos, ante todo, que todavía no conocemos si es resoluble el problema, es decir, si pueden moverse los hombres como lo requiere la condición del problema. En efecto, si a un cruce cualquiera, en que va a dividirse por mitad la afluencia de gente, llega un número impar de hombres, el movimiento se detendrá. Por consiguiente, para que el problema tenga solución, es necesario y suficiente que a cada cruce de cualquiera de las primeras mil series (filas), de 0 hasta 999, llegue un número par de hombres. De que esto es así, nos cercioraremos resolviendo el problema.

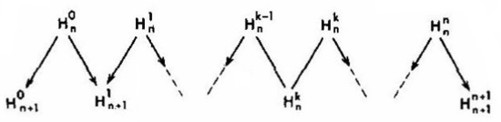
Al principio introduciremos las designaciones para las cantidades de hombres que dejaron atrás cada cruce de nuestra red de caminos. Numeremos los cruces de cada fila, de izquierda a derecha, partiendo de cero; por lo tanto, los cruces de la n-ésima fila se numerarán de cero hasta n. Denotaremos por Hkn el número de hombres que pasaron por el k-ésimo cruce de la n-ésima fila. Puesto que no se sabe todavía si es resoluble el problema, no podemos estar seguros de que existan todos los números Hkn, es decir, que exista cada uno de los números H con todo n de 0 hasta 1000 y todo k de 0 hasta n. Es indudable que algunos de ellos existen. De modo que, en virtud de las designaciones introducidas,

H00 = 21000 (1.1)

Veamos ahora cómo se vinculan entre sí los números Hkn (k = 0, 1, 2,..., n) y Hkn+1 (k = 0, 1, 2, ..., n+1) a condición de que existan todos. Más tarde veremos que si existen y son pares todos los números Hkn, existen también todos los números Hkn+1. Consideremos las filas n y (n + 1) de los cruces y los tramos de los caminos que los unen; pongamos frente a cada cruce la designación del número respectivo de hombres (véase la figura 2). El número de hombres que salieron del cruce 0 de la fila n (es decir, H0n) se dividirá en dos partes iguales y una mitad llegará al cruce 0 de la fila (n + 1); por eso,

H0n+1= H0n / 2 (1.2)

Otra mitad de H0n se aproximará al primer cruce de la fila (n + 1) y se reunirá allá con la mitad de hombres que han abandonado el primer cruce de la fila n, o sea, con la mitad

H1n.

De ahí

H1n+1 = (H0n + H1n)/2

En general, el número de hombres que llegaron al cruce k de la fila (n + 1) era la suma de mitad de hombres que partieron del cruce (k - 1) de la fila n (esta mitad era igual a Hk-1n /2) con la de hombres que partieron del cruce k de la fila n (esta mitad era igual a Hkn /2

Por 1 tanto,

Hkn+1=(Hk-1n + Hkn)/2 (1.3)

con 1 kn

Por fin, el número de hombres que alcanzaron el cruce (n + 1) de la fila (n + 1) es equivalente a la mitad de hombres que salieron del cruce n de la fila n:

Hn+1n+1=Hnn /2 (1.4)

Las relaciones (1.1) - (1.4) permiten establecer que el problema admite realmente su solución. En efecto, de las igualdades (1.2) - (1.4) se deduce que si con cierto n fijo todos los números de la fila a: H0n, H1n,..., Hnn existen y son divisibles por 2a, todos los números de la fila (n + 1): H0n+1, H1n+1..., Hn+1n+1 también existen y son divisibles por a. Por consiguiente, puesto que todos los números de la fila 0 (Su total es un solo H00 existen y son divisibles por 21000 (en virtud de (1.1), todos los números de la primera fila

H01, H11

existen y son divisibles por 2999; todos los números de la segunda fila

H02, H12, H22

existen y son divisibles por 2998; todos los números de la 999-ésima fila

H0999, H1999,...H999999

existen y son divisibles por 2; todos los números de la 1000-ésima fila

H01000, H11000,...H10001000

existen (y son divisibles por 2).

Las relaciones (1.2) - (1.4) no sólo demuestran que existe la solución del problema, sino que señalan cómo de una línea de números

H0n, H1n,... Hnn

se obtiene la otra

H0n+1, H1n+1,... Hn+1n+1

Empleando sucesivamente estas relaciones, a partir de la línea cero [es decir, aprovechando la relación (1.1)] podemos calcular, en principio, los valores de Hkn para todos los 501501 cruces, que se contienen en las filas hasta el milésimo inclusive, en particular, para todos los cruces de la milésima fila, resolviendo, por lo tanto, el problema. De manera que para las primeras filas por cálculo directo resulta:

H01= H00/2 = 21000/2 = 2999; H11= H00/2 = 21000/2 = 2999

H02= H01/2 = 2999/2 = 2998; H12= (H01+ H11)/2 = (2999 + 2999)/2 = 2999;

H22= H11/2 = 2999/2 = 2998; H03= H02/2 = 2998/2 = 2997;

H13= (H02+ H12)/2 = (2998 + 2999)/2 = 3 x 2997; etc

Capítulo 2

¿QUE SIGNIFICA RESOLVER EL PROBLEMA?

Por consiguiente, el problema del Capítulo 1 está resuelto...

¿Resuelto?, se sorprenderá un lector inexperto (ya que el experimentado sabe de antemano lo que va a decir el autor y no se sorprenderá por nada). "No he notado que lo hayamos resuelto”.

Autor. Está claro que lo hemos resuelto. Es que resolver el problema es hallar su solución. Ya lo hemos hecho.

Lector (perturbado). ¿Acaso es ésta la solución?

Autor (fingiéndose que no entiende en "qué consiste" el asunto) ¿Y qué, es errónea la solución?

Lector. No, es cierta, pero, en general, no es la solución.

Autor. Pues, ¿qué significa la solución?

Lector. Una línea de números que señalen cuántos hombres llegarán a los cruces de la milésima fila.

Autor. Pero, esta línea ha de contener 1001 números. ¿Acaso los organizadores de la VIII Olimpíada tenían esperanza en que alguien les escribiera el número 1001?