CK-12 Geometría, Volumen 1
To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
No more static textbooks! CK-12 Foundation updates all its FlexBooks on a regular basis. Please visit us at www.ck12.org to access the latest version of this FlexBook and to see previews of coming attractions.
CK-12 Foundation is a non-profit organization with a mission to reduce the cost of textbook materials for the K-12 market both in the U.S. and worldwide. Using an open-content, web-based collaborative model termed the FlexBook®. CK-12 intends to pioneer the generation and distribution of high-quality educational content that will serve both as core text as well as provide an adaptive environment for learning, powered through the FlexBook Platform®.
Copyright © 2011 CK-12 Foundation, www.ck12.org
The names "CK-12" and "CK12" and associated logos and the terms "FlexBook®" and "FlexBook Platform®" (collectively "CK-12 Marks") are trademarks and service marks of CK-12 Foundation and are protected by federal, state and international laws.
Any form of reproduction of this book in any format or medium, in whole or in sections must include the referral attribution link http://www.ck12.org/saythanks (placed in a visible location) in addition to the following terms.
Except as otherwise noted, all CK-12 Content (including CK-12 Curriculum Material) is made available to Users in accordance with the Creative Commons Attribution/Non-Commercial/Share Alike 3.0 Unported (CC-by-NC-SA) License (http://creativecommons.org/licenses/by-nc-sa/3.0/), as amended and updated by Creative Commons from time to time (the "CC License"), which is incorporated herein by this reference.
Complete terms can be found at http://www.ck12.org/terms.
ISBN :9781935983293
Say Thanks to Authors
Click http://ck12.org/saythanks
(No Sign in required)
Chapter 1: Bases de Geometría
Puntos, líneas y planos
Objetivos de enseñanza
- Comprender los términos indefinidos de punto, línea y plano.
- Comprender los términos definidos, incluyendo espacio, segmento y rayo.
- Identificar y aplicar postulados básicos de puntos, líneas y planos.
- Dibujar y enunciar términos en un diagrama.
Introducción
¡Bienvenido al excitante mundo de la geometría! Delante de ti encontrarás los descubrimientos más emocionantes que te ayudarán a aprender más sobre el mundo. La geometría es usada en muchas áreas, desde el arte hasta la ciencia. Por ejemplo, la geometría juega un papel clave en la construcción, diseño de modas, arquitectura y gráficos de computadora. Este curso se enfoca en las ideas principales de la geometría que son la base para su aplicación en todos los rubros. En este capítulo estudiarás los elementos básicos de geometría. Luego, probarás cosas acerca de las formas geométricas usando el vocabulario y las ideas de este capítulo, para estar seguros de que comprendes completamente cada uno de los conceptos presentados aquí y, así, poder continuar.
Términos indefinidos
Los tres bloques constructivos de la geometría son los puntos, las líneas y los planos. Estos son términos indefinidos. Ya que no podemos definir estos términos con precisión, nos podemos hacer una idea de su significado mediante ejemplos y modelos.
Un punto es una ubicación que no tiene tamaño. Para imaginar lo que es un punto, mira el punto ortográfico al final de esta oración. Ahora imagina que se hace cada vez más y más pequeño hasta que desaparece. Un punto describe una ubicación, como el lugar donde está ubicado este punto ortográfico, pero no tiene tamaño. Usamos pequeños círculos para representar los puntos, pero ya que los puntos no ocupan espacio, estos círculos no son puntos, solo son su representación. Los puntos se designan con una letra mayúscula, como se muestra a continuación.

Una línea es una sucesión continua de puntos. Una línea no ocupa espacio, así que piensa en el hilo más delgado que puedas imaginar y, luego, imagina que este se hace cada vez más delgado hasta que ya no ocupa espacio. Una línea tiene ubicación y dirección, pero no ocupa espacio. A veces nos referimos a las líneas mediante letras en cursiva, pero también pueden ser identificadas mediante dos puntos contenidos en ella. Las líneas son llamadas unidimensionales, ya que solo tienen dirección en una dimensión.

El último término indefinido es el plano. Puedes pensar en un plano como una hoja de papel gigante, ¡tan grande que llega al infinito! Imagina que este papel es tan delgado como sea posible y se extiende hacia arriba y hacia abajo, hacia la izquierda y a la derecha. Podemos nombrar a los planos mediante letras, o mediante tres puntos que pertenezcan al plano. Tú ya conoces un plano de tu clase de álgebra —el 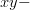 o plano cartesiano—. Los planos son llamados bidimensionales, ya que cualquier punto que se encuentre en un plano puede ser descrito mediante dos números, llamados coordenadas, como ya aprendiste en álgebra.
o plano cartesiano—. Los planos son llamados bidimensionales, ya que cualquier punto que se encuentre en un plano puede ser descrito mediante dos números, llamados coordenadas, como ya aprendiste en álgebra.
Notas: Cuando un nuevo término es introducido, las notas sobre notación te ayudarán a aprender cómo escribirlo y nombrarlo.
- Los puntos son nombrados mediante una letra mayúscula. La primera imagen muestra los puntos
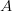 ,
, 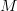 y
y 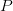 .
. - En la imagen de una línea, la misma línea tiene varios nombres. Puede ser llamada "línea
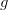 ,"
," 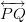 o
o 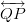 . El orden de las letras no importa cuando nombramos una línea, de manera que esta puede tener varios nombres. Cuando usamos dos puntos para nombrarla debes usar el símbolo de línea
. El orden de las letras no importa cuando nombramos una línea, de manera que esta puede tener varios nombres. Cuando usamos dos puntos para nombrarla debes usar el símbolo de línea  sobre las letras.
sobre las letras. - Los planos son nombrados usando una letra cursiva o nombrando tres puntos contenidos en él. El plano ilustrado puede ser llamado plano
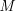 o “el plano definido por los puntos
o “el plano definido por los puntos 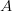














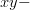 o plano cartesiano—. Los planos son llamados bidimensionales, ya que cualquier punto que se encuentre en un plano puede ser descrito mediante dos números, llamados coordenadas, como ya aprendiste en álgebra.
o plano cartesiano—. Los planos son llamados bidimensionales, ya que cualquier punto que se encuentre en un plano puede ser descrito mediante dos números, llamados coordenadas, como ya aprendiste en álgebra.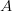 ,
, 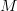 y
y 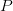 .
.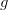 ,"
," 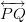 o
o 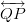 . El orden de las letras no importa cuando nombramos una línea, de manera que esta puede tener varios nombres. Cuando usamos dos puntos para nombrarla debes usar el símbolo de línea
. El orden de las letras no importa cuando nombramos una línea, de manera que esta puede tener varios nombres. Cuando usamos dos puntos para nombrarla debes usar el símbolo de línea  sobre las letras.
sobre las letras.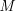 o “el plano definido por los puntos
o “el plano definido por los puntos