Alan Guth - El universo inflacionario

La energía negativa de un campo gravitatorio es decisiva para la idea de un universo de energía cero, por lo que es un tema que merece la pena examinar detenidamente. En este apéndice explicaré cómo pueden usarse las propiedades de la gravedad para demostrar que la energía de un campo gravitatorio es inequívocamente negativa. El razonamiento se expondrá en el contexto de la teoría de la gravitación de Newton, aunque se puede llegar a la misma conclusión usando la teoría de la relatividad general de Einstein.

Una manera sencilla de demostrar el signo de la energía gravitatoria consiste en imaginar una bóveda esférica laminar de masa, tal como se representa en la figura A.1 (a). La bóveda creará un campo gravitatorio, en el que cada punto del espacio proporciona una medida de la fuerza que experimentaría una masa si estuviera situada en ese punto. El campo gravitatorio puede calcularse usando los métodos de Newton. Newton examina primero una masa puntual ideal, una concentración de masa que es tan pequeña que puede considerarse como si toda la masa estuviera situada en un solo punto del espacio. Para este caso, el campo gravitatorio apunta directamente hacia la masa con una fuerza que viene definida por la ley de la inversa del cuadrado, es decir, la fuerza decrece proporcionalmente al cuadrado de la distancia a partir de la masa puntual. Para un objeto más complejo como la bóveda de la figura A.1 (a), el campo gravitatorio se determina en principio mediante la división mental del objeto en un número infinito de masas puntuales, cada una con una masa infinitamente pequeña. Una ilustración esquemática de esta división en masas puntuales se representa en la parte (b) de la figura. Para cada masa puntual se usa la sencilla ley de la inversa del cuadrado, y después hay que agregar el infinito número de contribuciones para obtener la respuesta final. La técnica para manejar este número infinito de cantidades es el objeto principal de lo que se llama cálculo integral, que fue desarrollado en gran medida por el propio Newton.

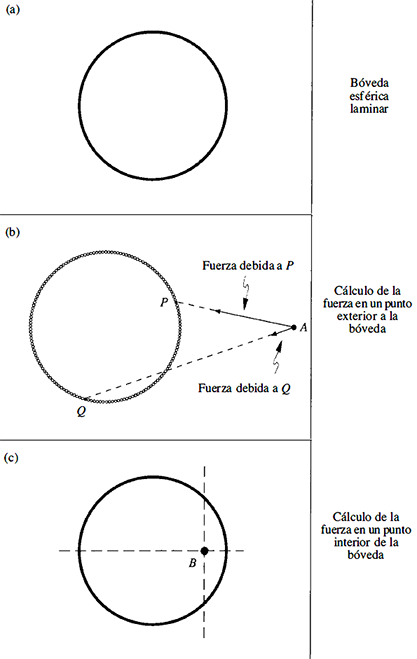
Figura A.1. El campo gravitatorio de una bóveda laminar esférica. La parte (a) representa la bóveda laminar. La bóveda es en realidad una esfera tridimensional, pero el gráfico sólo representa una sección bidimensional a través del centro de la esfera. En la parte (b) la bóveda ha sido dividida en un gran número de masas puntuales, con el fin de calcular el campo gravitatorio en el punto A. En principio, debería haber un número infinito de puntos de masa, pero sólo puede representarse un número finito. Las flechas indican la atracción gravitatoria hacia los puntos de masa rotulados P y Q. La atracción hacia P es más grande, porque está más cerca. La parte (c) representa un punto B, dentro de la cavidad esférica, en el que el campo gravitatorio ha de ser calculado. La masa situada a la derecha de la línea discontinua vertical está más cerca que la masa de la izquierda, pero hay más masa a la izquierda.

El resultado para el campo gravitatorio de una bóveda de masa fue calculado por vez primera por Newton, y es el tipo de cálculo que probablemente aparezca en cualquier curso de física de nivel universitario. Newton descubrió que, fuera de la bóveda, el campo gravitatorio en cualquier punto se dirige radialmente al interior hacia el centro de la bóveda. Esta respuesta podría haberse previsto a partir de la simetría del problema: no hay otra respuesta razonable a la pregunta «¿qué dirección podría señalar?». La fuerza del campo gravitatorio fuera de la bóveda puede definirse con sorprendente sencillez: el campo gravitatorio tiene exactamente la misma fuerza que tendría si toda la masa se concentrase en el punto central de la bóveda.

¿Cómo es el campo gravitatorio dentro de la bóveda esférica? Pensemos, por ejemplo, en la fuerza de una partícula situada en la posición B, tal como se representa en la parte (c). Por simetría, la fuerza estará a lo largo de la línea discontinua horizontal, porque la fuerza ascendente causada por la atracción hacia la masa en la mitad superior del diagrama será anulada por una atracción descendente opuesta hacia la masa en la mitad inferior del diagrama. Debemos decidir aún, sin embargo, si la fuerza apuntará a la derecha o a la izquierda. Hay un argumento convincente que dice que la fuerza debería apuntar a la derecha: puesto que la materia de la derecha está mucho más cerca que la materia de la izquierda, la ley del cuadrado inverso debería significar que la atracción hacia la materia de la derecha debería dominar. Hay también un argumento convincente que dice que la fuerza debería apuntar a la izquierda: hay más materia a la izquierda, por lo que la atracción hacia ella debería dominar.

¿Cuál de los argumentos del párrafo anterior es correcto? Newton demostró que estos dos argumentos son igualmente válidos, y de hecho las fuerzas se anulan exactamente para una partícula situada en cualquier punto dentro de la cavidad esférica.

Para continuar con el análisis de la energía gravitatoria, debernos responder a otra pregunta: ¿cómo afectaría la gravedad a la propia bóveda esférica? Cada punto de la bóveda esférica será atraído gravitatoriamente hacia cada uno de los otros puntos de la bóveda, y el efecto global es una fuerza que atrae a cada punto hacia el centro de la esfera. Si la materia de la que la bóveda está construida es blanda y comprimible, la gravedad hará que la bóveda se contraiga.

La situación se ilustra en la figura A.2, donde la parte (a) representa la bóveda laminar y el campo gravitatorio que genera. Fuera de la bóveda, el campo gravitatorio apunta hacia el interior, y, dentro, el campo gravitatorio es cero. Imaginemos ahora qué sucedería si se dejara que la bóveda se contrajera uniformemente, manteniendo su forma esférica. Se puede imaginar, por ejemplo, que se extrae la energía atando cuerdas a cada fragmento de la bóveda, como se ilustra en la parte (b). Estas cuerdas pueden usarse para impulsar generadores eléctricos a medida que cada fragmento es bajado hasta su nueva posición. La parte (c) representa la esfera después de alcanzar el nuevo radio. El círculo discontinuo indica el radio original de la bóveda, y fuera del círculo discontinuo el campo gravitatorio es idéntico al de la parte (a). (Recordemos que el campo en el exterior es igual que si toda la masa se concentrase en el centro, por lo que no depende del radio de la bóveda). Dentro de la bóveda en su nueva posición, el campo gravitatorio sigue siendo cero. Sin embargo, en la región sombreada entre las posiciones original y nueva de la bóveda, existe ahora un campo gravitatorio donde antes no existía campo alguno. El efecto global de esta operación es extraer energía y crear una nueva región de campo gravitatorio. Así pues, se libera energía cuando se crea un campo gravitatorio. La energía contenida en la región sombreada debe disminuir, pues, del mismo modo que el nivel del agua de un depósito disminuye si se deja salir agua. Puesto que la región comenzó sin campo gravitatorio alguno y por tanto sin energía, la energía final debe ser negativa. En la mayoría de los procesos físicos, el intercambio de energía gravitatoria es mucho más pequeño que la energía en reposo (mc2) de las partículas que intervienen, pero cosmológicamente la energía gravitatoria total puede ser muy importante.

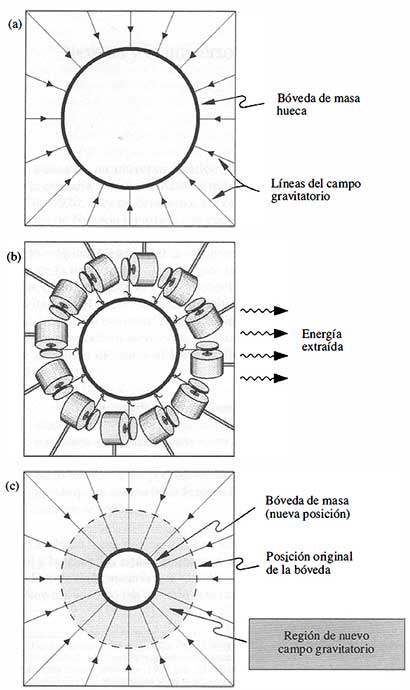
Figura A.2. Experimento mental para comprender la energía de la gravedad. La parte (a) representa una bóveda esférica laminar de masa y las líneas de campos gravitatorios que produce. Hay una fuerza en cada fragmento de la bóveda, que tira hacia el interior. La parte (b) representa cómo se puede extraer la energía a medida que se deja que la bóveda se contraiga uniformemente. Cada fragmento de la bóveda está unido por una cuerda a un generador eléctrico, que produce energía a medida que el fragmento es «bajado» hacia su posición final. La parte (c) representa la configuración final, que incluye un campo gravitatorio en la región sombreada donde antes no existía campo alguno. Así pues, la creación del campo gravitatorio está asociada a la liberación de energía.