Theoni Pappas
La Magia de la Matemática
El orden oculto tras la naturaleza y el arte
Divulgación
Este libro está dedicado a los matemáticos que han creado y siguen creando la magia de la matemática.
Colección dirigida por Jaime Poniachik y Daniel Samoilovich
Edición a cargo de Diego Uribe
Traducción de Mirta Rosenberg
© 1994 by Theoni Pappas
Edición original en inglés publicada por Wide World Publishing/ Tetra con el título The Magic of Mathematics.
© 1996 by Juegos & Co.
Edición digital: Sargont (2019)
I.S.B.N.: 84-88155-47-6
Depósito Legal: M. 23107-1996
Impreso en España - Printed in Spain
PREFACIO
No es necesario resolver problemas ni ser matemático para descubrir la magia de la matemática. Este libro es una compilación de ideas... ideas en las que subyace un tema matemático. No es un libro de texto. El lector no debe esperar convertirse en un experto en algún tema ni agotar una idea. La magia de la matemática investiga el mundo de las ideas, explora la seducción que la matemática ejerce sobre nuestras vidas, y ayuda al lector a descubrirla en los lugares más inesperados.
Muchos creen que la matemática es una disciplina rígidamente establecida. Nada podría estar más lejos de la verdad. La mente humana constantemente crea ideas matemáticas y mundos fascinantes y nuevos independientes de nuestro mundo... y rápidamente esas ideas se conectan con nuestro mundo, casi como si las hubieran tocado con una varita mágica. Del mismo modo en que los objetos de una dimensión pueden desaparecer en otra, siempre se puede encontrar un nuevo punto entre otros dos puntos cualesquiera, los números pueden producir operaciones, resolver ecuaciones, los gráficos pueden producir cuadros, el infinito resolver problemas, generar fórmulas... y todo eso parece poseer una cualidad mágica.
Las ideas matemáticas son creaciones de la imaginación. Son ideas que existen en mundos extraños, y sus objetos se producen mediante pura lógica y creatividad. Un círculo o un cuadrado perfectos existen en un mundo matemático, en tanto en nuestro mundo sólo existen representaciones de las cosas matemáticas.
Los tópicos y conceptos mencionados en cada capítulo no se limitan de ningún modo a esa sección. Por el contrario, los ejemplos pueden traspasar los límites arbitrarios de los capítulos. Aunque fuera posible, resultaría indeseable restringir una idea matemática a un área específica. Sin embargo, cada tópico es esencialmente completo, y puede ser disfrutado independientemente. Espero que este libro sea una puerta de entrada a los mundos matemáticos.
Galería de grabados, por M.C. Escher
© 1996 M.C. Escher/Cordon Art, Baarn, Holanda.
LA MATEMÁTICA EN LAS COSAS COTIDIANAS
La matemática del vuelo
La matemática de una llamada telefónica
Reflectores parabólicos y los faros de su auto
La complejidad y el presente
La matemática y la cámara
Reciclado de números
Bicicletas, mesas de pool y elipses
En busca de teselados
Sellos matemáticos
La cola del ratón
Una visita matemática
La ecuación del tiempo
¿Por qué las bocas de inspección de desagües son redondas?
No hay rama de la matemática, por abstracta que sea, que no pueda aplicarse algún día a los fenómenos del mundo real.
Nikolai Lobachevsky
Muchísimas de las cosas con las que estamos en contacto en nuestra rutina diaria tienen una base o una conexión matemática. Estas cosas oscilan entre volar en avión hasta la forma de las bocas de inspección de desagües. Con frecuencia, donde uno menos lo espera, descubrimos la presencia de la matemática. He aquí un muestreo al azar de esos casos.

LA MATEMÁTICA DEL VUELO
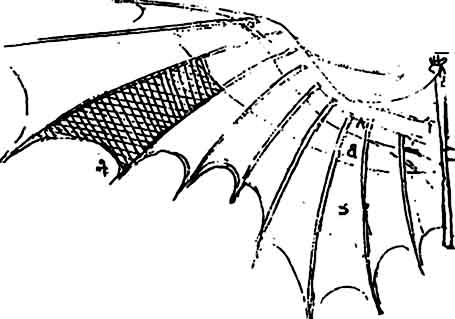
| Bocetos de los cuadernos de Leonardo da Vinci |

|
Leonardo da Vinci escribió: “...el hombre... podría someter el aire y elevarse en él con grandes alas de su propia creación. Una cosa ejerce contra el aire tanta fuerza como el aire ejerce contra ella” |
La gracia y naturalidad del vuelo de los pájaros han sido siempre un tormento para el deseo humano de volar. Las antiguas historias de muchas culturas dan testimonio del interés mostrado por diversas criaturas voladoras. Al ver los planeadores, advertimos que el vuelo de Dédalo y de Ícaro tal vez no fuera tan sólo un mito griego. Hoy, aeroplanos de enormes dimensiones se elevan con su carga al reino de los pájaros. Los peldaños históricos hasta que la humanidad consiguió volar, tal como ahora lo hacemos, han tenido literalmente sus altibajos. En el curso de los años, científicos, inventores, artistas, matemáticos y otros especialistas se han sentido desafiados ante la idea de volar, y han creado diseños, prototipos y experimentos con el objeto de dominar el aire.
He aquí un resumen condensado de la historia del vuelo:
* Los chinos inventaron las cometas (400-300 A.C.).
* Leonardo da Vinci estudió científicamente el vuelo de los pájaros y boceto diversas máquinas voladoras (1500).
* El matemático italiano Giovanni Borelli demostró que los músculos humanos son demasiado débiles para propulsar el vuelo (1680).
* El francés Jean Pilàtre de Rozier, marqués d’Arlandes, realizó el primer ascenso en globo de aire caliente (1783).
* El inventor británico, Sir George Cayley, diseñó el plano aerodinámico (sección transversal) de un ala, construyó y voló (1804) en el primer modelo de planeador, y fundó la ciencia de la aerodinámica.
* El alemán Otto Lilienthal ideó un sistema para medir la fuerza de sustentación producida por alas experimentales y realizó los primeros vuelos tripulados de planeadores entre 1891 y 1896.
* En 1903, Onille y Wilbur Wright realizaron los primeros vuelos tripulados en un aeroplano impulsado a motor. Experimentaron con tímeles de viento y sistemas de peso para medir la sustentación y la resistencia al avance de los modelos. Perfeccionaron las máquinas y las técnicas de vuelo, al punto que para 1905, sus vuelos alcanzaron los 38 minutos de duración, cubriendo una distancia de 20 millas.
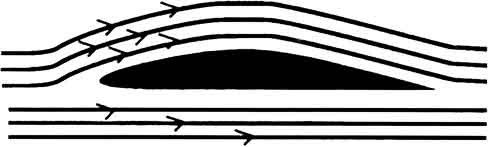
He aquí el modo en que nos elevamos del suelo:
explica el modo en que la forma de un ala crea una fuerza de ascenso. La parte superior del ala es curva.
Esa curva aumenta la velocidad del aire, y por lo tanto disminuye la presión del aire que pasa por encima de ella. Como la parte inferior del ala no tiene esta curva, la velocidad del aire que pasa por debajo del ala es menor, y por lo tanto su presión es mayor. La alta presión del aire debajo del ala se desplaza o empuja hacia la baja presión del aire que está por encima del ala, y de ese modo eleva al aeroplano. El peso (la fuerza de gravedad) es la fuerza vertical que contrarresta el ascenso del aeroplano.
La forma del ala hace más larga la distancia de la parte superior, lo que implica que el aire debe desplazarse más rápido sobre ella, haciendo que la presión del aire en la parte superior del ala sea menor que debajo del ala. La mayor presión existente debajo del ala empuja a ésta hacia arriba.