El Encanto
de la Matemática
Theoni Pappas
Colección dirigida por Jaime Poniachik y Daniel Samoilovich
Edición a cargo de Diego Uribe
Este libro está dedicado a los matemáticos
que han creado y siguen creando
la magia de la matemática.
Escaneado: Jacgarper
Edición digital: Sargont (2019)
Traducción de Mirta Rosenberg
© 1994 by Theoni Pappas
Edición original en inglés publicada por Wide World Publishing/Tetra con el título The Magic of Mathematics.
© 1996 by Juegos & Co. - Buenos Aires, Argentina
© 1996 by Zugarto Ediciones SA - Madrid, España
I.S.B.N.: 84-88155-51-4
Depósito Legal: M. 1387 - 1997
Impreso en España - Printed in Spain
No es necesario resolver problemas ni ser matemático para descubrir el encanto de la matemática. Este libro es una compilación de ideas... ideas en las que subyace un tema matemático. No es un libro de texto. El lector no debe esperar convertirse en un experto en algún tema ni agotar una idea. El encanto de la matemática investiga el mundo de las ideas, explora la seducción que la matemática ejerce sobre nuestras vidas, y ayuda al lector a descubrirla en los lugares más inesperados. Así, este libro continúa el enfoque ya iniciado en La magia de la matemática.
Los tópicos y conceptos mencionados en cada capítulo no se limitan de ningún modo a esa sección. Por el contrario, los ejemplos pueden traspasar los límites arbitrarios de los capítulos. Aunque fuera posible, resultaría indeseable restringir una idea matemática a un área específica. Sin embargo, cada tópico es esencialmente completo, y puede ser disfrutado independientemente. Espero que El encanto de la matemática sea una puerta de entrada a los mundos matemáticos.

MAGIA MATEMATICA DEL PASADO
Los babilonios y la raíz cuadrada
La escalera que asciende sobre 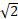
El método chino de apilar cuadrados
Los primeros generadores de números arbitrarios
La multiplicación egipcia
El primer laboratorio científico
Platón duplica el cuadrado
Los romanos y la superficie del círculo
Cómo el gnomon trisecciona un ángulo
Misterios matemáticos no resueltos
El último teorema de Fermat
Galileo y la proporción
Los recipientes y la matemática
Geometrías... viejas y nuevas
¿Qué hay en un nombre?
La fórmula mágica de Euler... F+V–E = 2
En casi todas las ciencias, una generación destruye lo que otra ha construido, y lo que una ha establecido, otra lo deshace. Sólo en la matemática cada generación añade un nuevo piso a la vieja estructura.
Hermann Hankel
En esta época de conflicto entre los estudios modernos y los antiguos, sin duda hay mucho que decir a favor de un estudio que no empezó con Pitágoras y que no terminará con Einstein, y que es el más antiguo y el más joven de todos.
G. H. Hardy
El descubrimiento de la magia matemática no se limita a la actualidad. Las historias e ideas del pasado son muy ricas en ella. Con frecuencia nos preguntamos de qué modo los antiguos usaron ideas tales como los números irracionales, las demostraciones, las secciones cónicas. Si no fuera por la curiosidad humana y por el deseo de aprender, ¿hubiera progresado la matemática hasta el lugar que ocupa en la actualidad? Este capítulo presenta unas pocas de la multitud de ideas matemáticas que han emergido en el transcurso de los siglos.
 Pascal probabilidad Laplace & Chu Shin-Chieh Pascal probabilidad Laplace & Chu Shin-Chieh
Zenón paradojas Whitehead • Einstein relatividad Liber Abaci Fibonacci serie 1, 1, 2, 3, 5, 8,... al Khwarizmi algebra Bhaskara lado + lado = hipotenusa Pitágoras a + b = c teoría de conjuntos Cantor números transfinitos Babbage ordenadores Lovelace programación Loyd acertijos Dudeney • Descartes coordenadas cartesianas Napier logaritmos • calculadora Pascal & Leibnitz Apolonio cónicas Hypatia Newton cálculo Leibnitz & Seki Kowa Agnesi curvas & análisis Noether • Diofanto ecuaciones Eratóstenes medida de la tierra Euclides geometrías Riemann & Bolyai & Lobachevsky |
Collage de ideas matemáticas y sus creadores

HINDO-ARÁBIGO • BABILONIO • GRIEGO • JEROGLÍFICO EGIPCIO • IDEOGRAMAS CHINOS • HEBREO • NÚMEROS CHINOS DE VARITAS • ROMANO • HIERÁTICO EGIPCIO • MAYA • NÚMEROS BINARIOS |
La historia nos muestra que la creatividad matemática no es privilegio de ninguna cultura en particular, de ninguna época, civilización ni género. La cantidad de ideas y contribuciones sorprendentes producidas con el transcurso de los siglos es verdaderamente increíble, y resulta muy excitante explorarlas. Esa exploración llevará al lector en un viaje a través del tiempo y de todos los países del mundo. Y ese viaje revelará que algunas ideas fueron descubiertas casi simultáneamente en diferentes países, como ocurrió con la geometría hiperbólica. Sabemos que los números y alguna forma de sistema numérico son inherentes a todos los pueblos. Descubrimos que el uso del cero y de la posición del número para representar el valor fueron desarrollados en muchas partes del mundo... primero por los babilonios, con su base 60, luego por los mayas con un sistema de base 20 modificada, y por los hindúes cuando desarrollaron una notación posicional para el sistema de base 10. Descubrimos que ese sistema fue más tarde mejorado y normalizado por los árabes. Los chinos también tenían un sistema de valor posicional y usaron el cero con sus numerales varitas, que más tarde perfeccionaron hasta lograr un sofisticado sistema de numeración decimal usado especialmente para resolver cálculos. En este capítulo sólo mencionamos a unos pocos matemáticos y unas pocas ideas de los muchos miles que existen. Los mencionados de ninguna manera son superiores o más importantes que los que no aparecen. Insto a los lectores a que usen estas secciones como trampolines y base para estudios más profundos, y para posibilitar la comprensión de la magia matemática del pasado. Con ese espíritu se ofrecen las ilustraciones con listas de matemáticos famosos, el collage de matemáticos y sus ideas, y el diagrama de los sistemas numéricos. Nos encontramos en medio de muchos descubrimientos matemáticos nuevos. No es necesario ser matemático para entender la esencia de estas ideas ni para apreciar su creatividad. Debemos buscar la magia matemática en el pasado y en el presente.
FERMAT | POINCARÉ | DU CHATELET | EUCLIDES |
EULER | BHASKARA | RAM ANU JAN | NOETHER |
PLATÓN | RIEMANN | LOBACHEVSKI | l-HSING |
PASCAL | LEIBNIZ | ARQUÍMEDES | LAGRANGE |
GALOIS | HILBERT | OMAR KHAYYAM | CAUCHY |
CAYLEY | DEDEKIND | FIBONACCI | EUXODO |
PAPPO | DESCARTES | KRONECKER | JACOBI |
TALES | BOOLE | KOVALESKAYA | SÓCRATES |
CANTOR | |















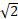
 Pascal probabilidad Laplace & Chu Shin-Chieh
Pascal probabilidad Laplace & Chu Shin-Chieh