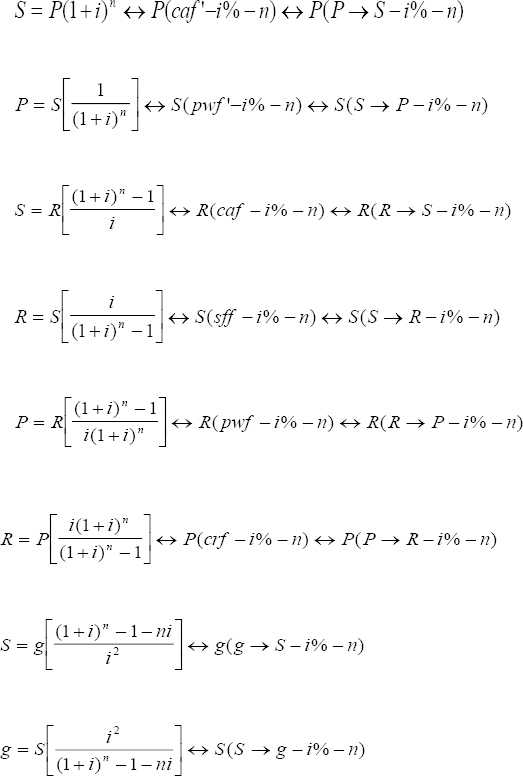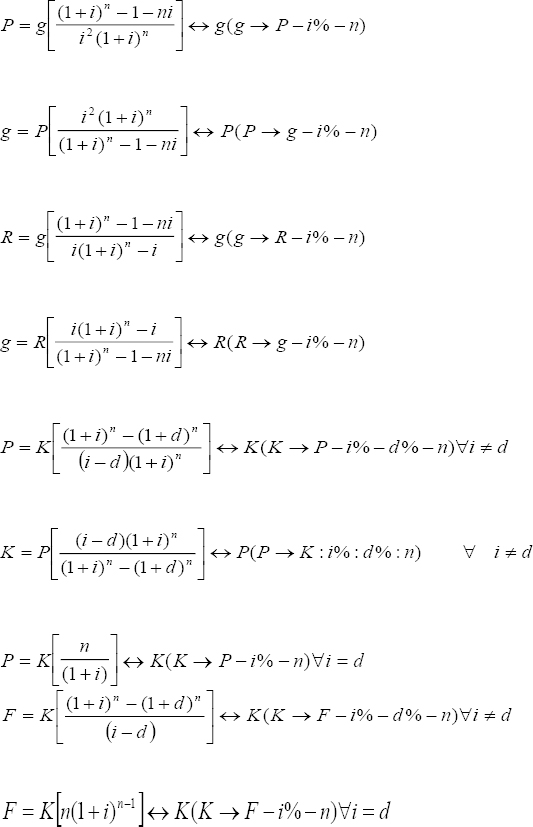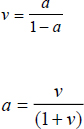Los tres principios fundamentales de las matemáticas financieras
son:
A1. Principio del valor cambiante del dinero a través del tiempo: cantidades de dinero en períodos diferentes de tiempo no se pueden sumar ni comparar, sino a través de los procedimientos de la estructura de las matemáticas financieras.
A2. Principio o criterio de equivalencia: la utilización del concepto de interés, el principio de equivalencia y la estructura matemática permiten la comparación de dineros localizados en períodos diferentes de tiempo.
A3. Principio de final de período: cuando se dice que un valor está localizado en el período r, significa que está localizado al final de este período, o sea, al principio del período r + 1.
B1. Interés (I): costo que hay que pagar por utilizar dinero ajeno a través del tiempo.
B2. Tasa de interés: costo que hay que pagar por utilizar la unidad monetaria de dinero ajeno a través de la unidad de tiempo.
B3. Valor presente o principal (P): se utiliza la letra P para designar una variable financiera que recibe el nombre de principal o valor presente. Se da este nombre a una cantidad única de dinero localizada en el período cero.
B4. Monto o valor futuro (S o F): se utilizan las letras S o F para denominar una variable financiera que recibe el nombre de monto o valor futuro y que es una cantidad única de dinero localizada en el período N.
B5. Renta (R): se utiliza la letra R para denominar una variable financiera que recibe el nombre de renta y que está constituida por una sucesión de valores aritméticamente iguales localizados a intervalos iguales de tiempo, de un período, de los cuales el primero está localizado en el período 1, el segundo en el 2, el tercero en el 3 y así sucesivamente, hasta el último que está localizado en el período N.
B6. Gradiente aritmético (g): se utiliza la letra g minúscula para denominar una variable financiera que recibe el nombre de gradiente aritmético y que está constituido por una sucesión de valores localizados a intervalos iguales de tiempo, de un período, de los cuales el primero está localizado en el período 2 y vale g; el segundo está localizado en el periodo 3 y es el doble del primero, por lo tanto vale 2g; el tercero está localizado en el periodo 4 y es el triple del primero, por lo tanto vale 3g, y así sucesivamente, hasta el último que está localizado en el período N y es igual a (N - 1) veces el primero, por lo tanto vale (N - 1)g.
B7. Gradiente geométrico (K): se utiliza la letra K para designar una variable financiera denominada gradiente geométrico, constituida por una sucesión de valores localizados a intervalos iguales de tiempo, de un período, y que varían un (d%) por periodo a partir del periodo 2. Por lo tanto el primer valor está localizado en 1 y vale K; el segundo valor está localizado en 2 y vale K (1 + d); el tercero, está localizado en 3 y vale K (1 + d)2y así sucesivamente hasta que el último valor, está localizado en el período N y vale K (1 + d)(N-1)
C1. El valor presente o principal siempre está localizado en cero, P ↓ 0.
C2. El monto o valor futuro está localizado en N, S ↓ N.
C3. 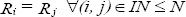 lo cual se lee “la renta localizada en i es igual a la renta localizada en j para todos i y j pertenecientes al conjunto de los números naturales menores o iguales a N”.
lo cual se lee “la renta localizada en i es igual a la renta localizada en j para todos i y j pertenecientes al conjunto de los números naturales menores o iguales a N”.
C4. 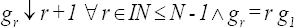 localizado en el período r + 1 para todo r perteneciente al conjunto de los números naturales menores e iguales que N - 1 y el gradiente de orden r es igual a r veces el gradiente 1, que está localizado en 2.
localizado en el período r + 1 para todo r perteneciente al conjunto de los números naturales menores e iguales que N - 1 y el gradiente de orden r es igual a r veces el gradiente 1, que está localizado en 2.
C5. 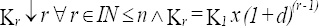 lo cual se lee “el gradiente geométrico de orden r está localizado en el período r para todo r perteneciente al conjunto de los números naturales menores e iguales a N y el gradiente de orden r es igual al gradiente de orden 1 multiplicado 1 + una tasa de crecimiento elevado a la potencia N - 1.
lo cual se lee “el gradiente geométrico de orden r está localizado en el período r para todo r perteneciente al conjunto de los números naturales menores e iguales a N y el gradiente de orden r es igual al gradiente de orden 1 multiplicado 1 + una tasa de crecimiento elevado a la potencia N - 1.
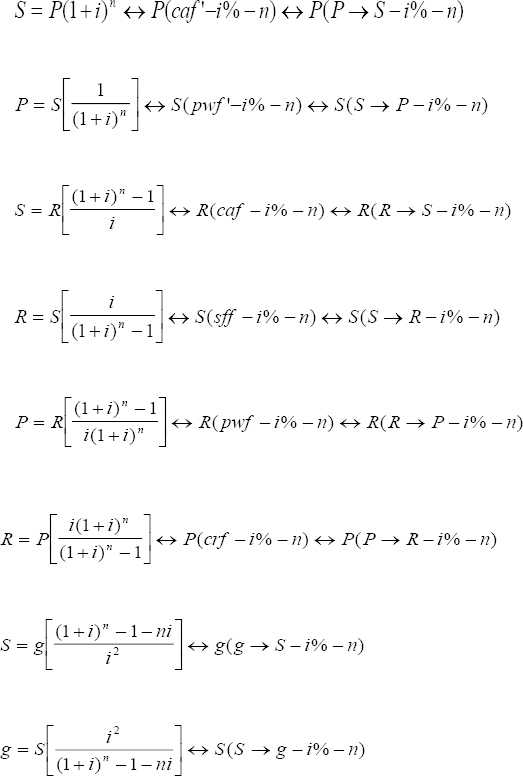
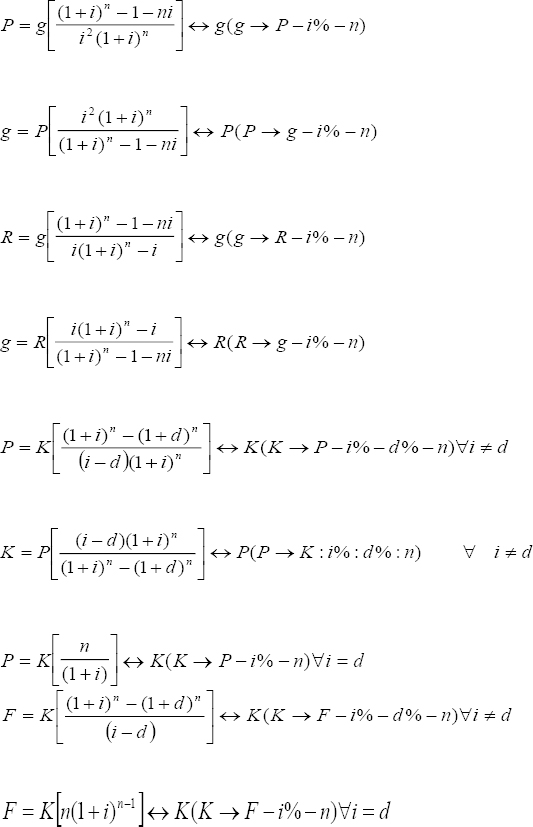
Conversión de tasas (anticipadas ↔ vencidas)
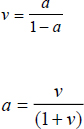
Procedimiento para conversión de tasas de interés:

1. $76.909.254,23
2. $81.438.245,57
3. $652.183,38
4. $4.865.967,69
5. $1.405.306,42
6. $69.690.322,14
7. $15.371.765,19
8. $631.067,96
9. 35,5034% anual
10. 20,0937% semestral
11. 46,5555 meses = 3 años, 10 meses y 17 días
12. $373.472,18
13. $1.051.744,13
14. $1.117.722,96
15. $2.590.905,71
16. $43.468.962,87
17. $4.204.594,09
18. $3.718.877,74
19. $170.889,18
20. $9.324.029,63
21. $99.511.010,48

23. $200.000.000
24. $743.338,76
25. $415.978
26. $6.673.492,57
27. $16.873.141,90
28. $4.824.484,44
29. $15.007.189,25
30. $38.378,27
31. $81.593,41
32. $1.819.238,84
33. $25.560.957,64
34. $3.287.187,96
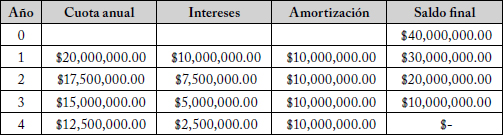
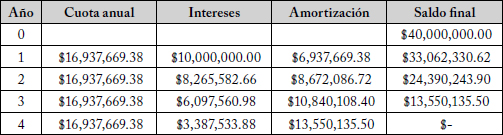
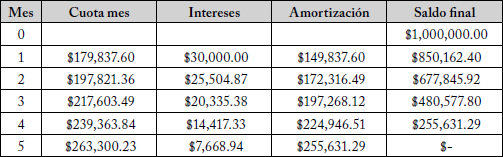
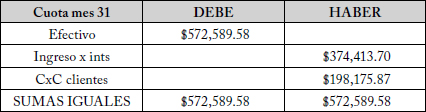

40. $138.000
41. $262.812,75

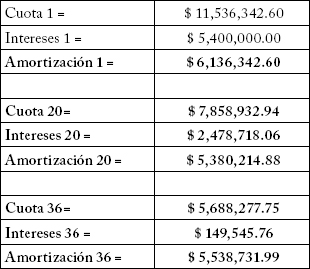
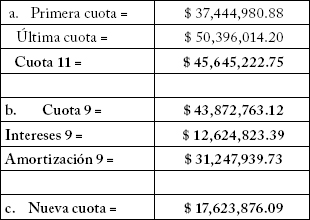














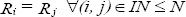 lo cual se lee “la renta localizada en i es igual a la renta localizada en j para todos i y j pertenecientes al conjunto de los números naturales menores o iguales a N”.
lo cual se lee “la renta localizada en i es igual a la renta localizada en j para todos i y j pertenecientes al conjunto de los números naturales menores o iguales a N”.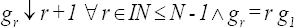 localizado en el período r + 1 para todo r perteneciente al conjunto de los números naturales menores e iguales que N - 1 y el gradiente de orden r es igual a r veces el gradiente 1, que está localizado en 2.
localizado en el período r + 1 para todo r perteneciente al conjunto de los números naturales menores e iguales que N - 1 y el gradiente de orden r es igual a r veces el gradiente 1, que está localizado en 2.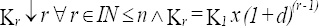 lo cual se lee “el gradiente geométrico de orden r está localizado en el período r para todo r perteneciente al conjunto de los números naturales menores e iguales a N y el gradiente de orden r es igual al gradiente de orden 1 multiplicado 1 + una tasa de crecimiento elevado a la potencia N - 1.
lo cual se lee “el gradiente geométrico de orden r está localizado en el período r para todo r perteneciente al conjunto de los números naturales menores e iguales a N y el gradiente de orden r es igual al gradiente de orden 1 multiplicado 1 + una tasa de crecimiento elevado a la potencia N - 1.