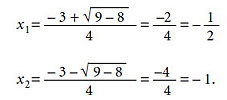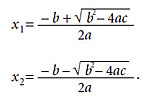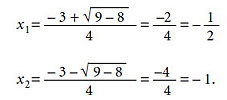Mario Livio - La proporción áurea

Queremos demostrar que por cada uno de los números enteros p y q, tales que p sea mayor que q, los tres números: p2 – q2;2pq y p2 + q2 forman un triplete pitagórico. En otra palabras, necesitamos demostrar que la suma de los cuadrados de los dos primeros es igual al cuadrado del tercero. Para esto, usaremos las identidades generales que funcionan tanto para a como para b:

(a + b)2 = (a + b)(a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2

(a – b)2 = (a – b)(a – b) = a2 – ab – ba + b2 = a2 – 2ab + b2.

Basándonos en estas identidades, el cuadrado del primer número es:

(p2 – q2)2 = p4 – 2p2q2 + q4

Y la suma de los dos primeros cuadrados es:

p4 – 2p2q2 + q4 + 4p2q2 = p4 + 2p2q2 + q4.

El cuadrado del último número es:

(p2 + q2)2 = p4 + 2p2q2 + q4.

Por tanto, podemos observar que el cuadrado del tercer número es realmente igual a la suma de los cuadrados de los dos primeros, sin importar los valores de p y q.

La demostración de Euclides de que existen muchos primos infinitos se basa en el método de la reducción ad absurdum. Empezó asumiendo la siguiente contradicción: sólo existe un número finito de números. Si eso fuera cierto, no obstante, entonces uno de ellos debe ser el primo más grande. Llámemos a ese primo P. Euclides construyó un nuevo número mediante este proceso: multiplicó todos los primos juntos desde el 2 hasta (e incluyendo) P, y entonces añadió 1 al producto. El nuevo número era

2 × 3 × 5 × 7 × 11 … × P + 1.

Dada la conclusión original, este número debe ser compuesto (no primo), porque obviamente es mayor que P, el cual hemos aceptado que es el número primo mayor. Por tanto, este número debe ser divisible por al menos uno de los primos existentes. De todas formas, dada su construcción, vemos que si dividimos este número por cualquier primo mayor de P, esto dejará un 1 como resto. La implicación es, que si el número es en realidad compuesto, algunos primos mayores de P deben dividirlo. De todos modos, esta conclusión contradice la afirmación según la cual P es el primo mayor; por tanto queda completada la demostración de que existe un número infinito de números primos.

Queremos demostrar que la diagonal y el lado del pentágono son inconmensurables, no tienen ninguna medida común.

La prueba es mediante el método general de la reductio ad absurdum descrita al final del capítulo 2.

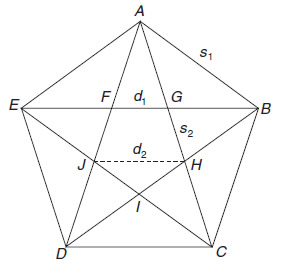
Llamemos s1 al lado del pentágono ABCDE y d1 a su diagonal. A partir de las propiedades del triángulo isósceles se demuestra fácilmente que AB = AH y HC = HJ. Llamemos ahora s2 al lado del pentágono pequeño FGHIJ y d2 a su diagonal. Tendremos:

AC = AH + HC = AB + HJ.

Por tanto:

d1 = s1 + d2 o d1 – s1 = d2

Si d1 y s1 tienen una misma medida, significa que tanto d1 y s1 son múltiplos integrados de la misma medida. Por tanto, también es una medida común de d1 – s1, y por tanto de d2. De forma similar, las igualdades

AG = HC = HJ

AH = AB

y

AH = AG + GH AB = HJ + GH

nos dan

s1 = d2 + s2

o

s1 – d2 = s2.

Basándonos en nuestra presunción de que la medida común de s1 y d1 es también una medida común de d2, la última igualdad demuestra que también es una medida común de s2.Por tanto descubrimos que la misma unidad que mide d1 y s1 también mide d2 y s2. Este proceso continúa ad infinitum para pentágonos cada vez más pequeños. Obtendríamos que la misma unidad que tiene una medida común para el lado y diagonal del primer pentágono es también una medida común del resto de pentágonos, sin importar lo pequeños que fueran. Ya que esto no puede ser verdad, significa que nuestra presunción inicial según la cual el lado y diagonal tienen una medida común era falsa; esto completa la prueba de que d1 y s1 son inconmensurables.

El área de un triángulo es la mitad del producto de la base y de la altura a la base. En el triángulo TBC la base, BC, es igual a 2a y la altura, TA, es igual a s. Por tanto, el área del triángulo es igual a s × a. Queremos demostrar que si el cuadrado de la altura de la pirámide, h2, es igual al área de su cara triangular, s × a, entonces s/a es igual a la Proporción Áurea.

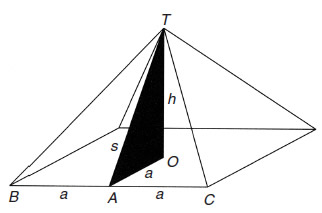
Tenemos

h2 = s × a.

Usando el teorema de Pitágoras en el triángulo rectángulo TOA, tenemos

s2 = h2 + a2.

Ahora podemos sustituir h2 de la primera ecuación para obtener

s2 = s × a + a2.

Dividiendo ambos lados por a2, obtenemos:

(s/a)2 = (s/a) + 1.

En otras palabras, si cambiamos s/a por x tenemos la ecuación cuadrática:

x2 = x + 1.

En el capítulo 4 muestro que ésta es precisamente la ecuación definida por la Proporción Áurea.

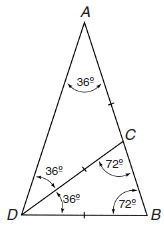
Uno de los teoremas de los Elementos demuestra que cuando dos triángulos tienen los mismos ángulos son semejantes. Es decir, los dos triángulos tienen exactamente la misma forma, con todos los lados proporcionales entre sí. Si un lado de un triángulo es el doble de largo que el de otro, entonces ocurre lo mismo con el resto de lados. Los dos triángulos ADB y DBC son semejantes (porque tienen los mismos ángulos). Por tanto, la proporción AB/DB (proporción de los lados de dos triángulos ADB y DBC) es igual a DB/BC (proporción de las bases de los dos triángulos):

AB/DB = DB/BC.

Pero los dos triángulos son también isósceles, así que

DB = DC = AC.

Por tanto, descubrimos a partir de las dos igualdades anteriores que

AC/BC = AB/AC,

lo que significa (según la definición de Euclides) que el punto C divide la línea AB en Proporción Áurea. Dado que AD = AB y DB = AC, también tenemos que AD/DB = Φ.

Las ecuaciones cuadráticas son ecuaciones del tipo

ax2 + bx + c = 0,

donde a, b y c son números arbitrarios. Por ejemplo, en la ecuación 2x2 + 3x + 1 = 0, a = 2, b = 3, c = 1.

La fórmula general para las dos soluciones de la ecuación es

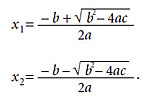
En el ejemplo anterior