Apéndices
Apéndice 1. La demostración del teorema de Pitágoras
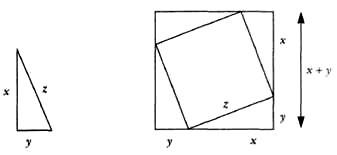
El propósito de la demostración es probar que el teorema de Pitágoras es cierto para todos los triángulos rectángulos. El triángulo mostrado arriba podría ser cualquier triángulo rectángulo ya que las longitudes de sus lados no están especificadas, sino representadas por las letras x, y y z.
En la figura de arriba se combinan cuatro triángulos rectángulos idénticos con un cuadrado girado para construir un cuadrado mayor. El área de este cuadrado mayor es la clave de la demostración.
El área del cuadrado se puede calcular de dos modos:
Método 1. Medir el área del cuadrado como un todo. La longitud de cada lado es x + y. Por lo tanto, el área del cuadrado grande es (x + y)²
Método 2. Medir el área de cada elemento del cuadrado grande. El área de cada triángulo es (½)xy, o sea, ½ × base × altura. El área del cuadrado girado es z². En consecuencia, área del cuadrado grande = 4 (área de cada triángulo) + área del cuadrado girado = 4 × ½xy + z².
Los métodos 1 y 2 dan dos expresiones diferentes. Sin embargo, estas dos expresiones deben ser equivalentes puesto que representan la misma área. Por ello,
área del método 1 = área del método 2
(x + y)² = 4 × ½xy + z².
Los paréntesis se pueden desarrollar y simplicar. Entonces,
x² + y² + 2xy = 2xy + z².
El termino 2xy se cancela en ambos lados. Así tenemos
x² + y² = z².
¡Qué es el teorema de Pitágoras!
La argumentación se basa en el hecho de que el área del cuadrado mayor debe ser la misma sin importar qué método se usa para calcularla. Entonces, por medio de la lógica, derivamos dos expresiones para la misma área, las igualamos, y finalmente la conclusión inevitable es que x² + y² = z², es decir, el cuadrado de la hipotenusa, z², es igual a la suma de los cuadrados de los catetos, x² + y².
Este razonamiento es cierto para todos los triángulos rectángulos. Los lados del triángulo en nuestro razonamiento están representados por x, y y z, y pueden, por lo tanto, representar los lados de cualquier triángulo rectángulo.
Apéndice 2. Demostración de Euclides de que √2 es irracional
El objetivo de Euclides era probar que √2 no se puede escribir como una fracción. Debido a que usó una reducción al absurdo, el primer paso es suponer que lo contrario es cierto, es decir, que √2 se podría escribir como alguna fracción desconocida. Esta hipotética fracción se representa por p/q, donde p y q son dos números enteros.
Antes de embarcarnos en la demostración en sí, todo lo que se requiere es una comprensión básica de algunas propiedades de las fracciones y los números pares.
- Si se toma cualquier número y se multiplica por 2, el nuevo número debe ser par. Esto es casi equivalente a la definición de un número par.
- Si se sabe que el cuadrado de un número es par, entonces el número mismo debe ser también par.
- Finalmente, las fracciones se pueden simplificar: 16/24 es lo mismo que 8/12; sólo hay que dividir el numerador y el denominador de 16/24 por el factor común 2. Es más, 8/12 es lo mismo que 4/6, y, a su vez, 4/6 es lo mismo que 2/3. Sin embargo, 2/3 no puede ser simplificado ya que 2 y 3 no poseen factores comunes. Es imposible continuar simplificando una fracción por siempre.
Ahora recuérdese que Euclides cree que √2 no se puede escribir como una fracción. Sin embargo adopta el método de prueba por contradicción y trabaja con la suposición de que la fracción p/q existe y explora las consecuencias de su existencia:
√2 = p/q.
Si se elevan ambos miembros al cuadrado, entonces
2 = p²/q².
Esta ecuación se puede reescribir como
2q² = p².
Ahora, según el punto 1, sabemos que p² debe ser par. Es más, por el punto 2 sabemos que el mismo p también ha de ser par. Pero si p es par entonces se puede escribir como 2m, donde m es otro número entero. Esto se sigue del punto 1. Lo introducimos en la ecuación y resulta
2q² = (2m)² = 4m².
Dividiendo ambos lados por 2, se tiene
q² = 2m².
Pero por el mismo argumento que el usado antes sabemos que q² ha de ser par, y así el mismo q también tiene que ser par. Si éste es el caso, entonces q se puede escribir como 2n, donde n es algún otro número entero. Si volvemos al principio, entonces
√2 = p/q = 2m/2n.
La fracción m/n se puede simplificar dividiendo el numerador y el denominador por 2, y se obtiene
√2 = m/n.
Ahora se tiene una fracción m/n que es más sencilla que p/q.
Sin embargo, nos encontramos en la posición de poder repetir exactamente el mismo proceso sobre m/n, y al final del proceso generaremos una fracción aún más sencilla, digamos g/h. Esta fracción puede ser pasada otra vez por la piedra del molino, y la nueva fracción, llamémosla e/f, será más simple aún. Podemos volver a tratar esta fracción y repetir el proceso una y otra vez, en una sucesión sin fin. Pero por el punto 3 sabemos que las fracciones no pueden simplificarse indefinidamente. Siempre existe la fracción más simple, pero nuestra fracción hipotética original p/q no parece obedecer esta regla. Por lo tanto, estamos justificados para decir que hemos encontrado una contradicción. Si √2 se pudiera escribir como una fracción la consecuencia sería un absurdo, y así lo correcto es decir que √2 no se puede escribir como una fracción. Por tanto √2 es un número irracional.
Apéndice 3. El enigma de la edad de Diofante
Llamemos L a la longitud de la vida de Diofante. A partir del acertijo tenemos la siguiente relación completa de la vida de Diofante:
1/6 de su vida, L/6, lo pasó siendo un niño,
L/12 lo pasó siendo un joven,
L/7 lo pasó antes de su matrimonio,
5 años después nació su hijo,
L/2 fue la duración de la vida de su hijo,
4 años pasó sumido en la pena antes de morir.
La longitud de la edad de Diofante es la suma de todo lo anterior:
L = L/6 + L/12 + L/7 + 5 + L/2 + 4.
Podemos simplificar la ecuación como sigue:
L = (25/28) L + 9
(3/28) L = 9
L = (28/3) × 9 = 84
Diofante murió a la edad de 84 años.
Apéndice 4. El problema de las pesas de Bachet
Para pesar cualquier número de kilogramos entre 1 y 40 la mayor parte de la gente sugeriría que se precisan seis pesas: 1, 2, 4, 8, 16 y 32 kg. De esta forma, todos los pesos se pueden obtener fácilmente colocando las siguientes combinaciones en un platillo:
| 1 kg | = 1, |
| 2 kg | = 2, |
| 3 kg | = 2 + 1, |
| 4 kg | = 4, |
| 5 kg | = 4 + 1, |
| ↓ |
| 40 kg | = 32 + 8. |
Sin embargo, si se sitúan pesas en ambos platillos, de forma que las pesas también puedan ponerse junto con el objeto pesado, Bachet pudo completar la tarea con sólo cuatro pesas: 1, 3, 9 y 27 kg. Una pesa situada en el mismo platillo que el objeto que se está pesando toma un valor efectivo negativo. Así, los pesos se pueden obtener como sigue:









