Luis Fernando Areán Álvarez - Fermat. El teorema de Fermat

LUIS FERNANDO AREÁN ÁLVAREZ (nacido en México Distrito Federal) es licenciado en Física por la Universidad Nacional Autónoma de México y Maestro en Ciencias por la Universidad de Stanford. Es un activo divulgador de la ciencia.

Imaginemos el instante. Un hombre de luengos cabellos se inclina, a la luz de una vela, sobre un ejemplar de la Aritmética del matemático griego Diofanto de Alejandría (ca. 214-ca. 298) con la espalda encorvada. Después de leer uno de los teoremas, reflexiona un poco, sonríe, moja la pluma y escribe una frase en latín en uno de los márgenes del libro. Hace una pausa, vuelve a tomar la pluma, y añade: «[…] cuius rei demonstrationem mirabilem sane detexi, hanc marginis exiguitas non caperet». Es decir: «[…] he encontrado una demostración admirable de este resultado, pero este margen es demasiado estrecho para escribirla».

Seguramente el hombre se iría pronto a dormir. Al día siguiente le esperaban urgentes asuntos en el Parlamento. No sabemos cuántas veces recordó esa pequeña anotación. Tal vez nunca volvió a pensar en ella; su vida estaba ocupada en otros menesteres. ¿Imaginó en algún momento que esas pocas palabras darían lugar a una de las más apasionantes odiseas de la historia de las matemáticas y que a lo largo de los siglos atormentarían a varias de las mentes más brillantes del mundo? Es poco probable. Pierre de Fermat, el protagonista de dicha escena, era dado a los juegos y las adivinanzas, pero es difícil suponer que aquella noche hubiera intuido que había creado la más famosa adivinanza matemática de todos los tiempos.

De hecho, tal adivinanza estuvo a punto de no pasar a la posteridad. Escrita como nota personal en el margen de un libro, pudo haber desaparecido sin más junto con los otros hechos más o menos triviales de una vida como tantas. Pero la acotación sobrevivió a su autor, fue descubierta e impresa, y se convirtió en el rey de los problemas al parecer imposibles de resolver. El mundo continuó su marcha. El cardenal Richelieu gobernaba la Francia que Alejandro Dumas inmortalizó en Los tres mosqueteros en la época en la que Fermat escribía, mientras un rey incapaz se recreaba en sus ocios. Cayó Richelieu, le siguieron la serie de movimientos de insurrección conocidos como la Fronda, el Rey Sol, y después la Ilustración, la Revolución, el revuelto siglo XIX y el aún más dramático siglo XX. Y mientras la historia discurría, el resultado que Fermat decía haber demostrado seguía ahí, resistiendo todos los ataques, todos los intentos para probarlo: esa demostración que no cabía en un margen tampoco tenía un lugar en las mentes de los más grandes matemáticos.

Aceleremos la acción. Nos encontramos ahora en 1993, un mundo con ordenadores y una red de Internet incipiente. La URSS había caído. No existían aún las redes sociales, pero sí un antecesor llamado Usenet, al que prácticamente solo estaban suscritas las personas ligadas al mundo académico, un número absurdamente pequeño si se compara con los actuales usuarios de determinadas redes sociales. De pronto, esa primitiva red, usualmente adormilada, comenzó a bullir de excitación. Los mensajes se sucedían, relampagueantes, con términos que un lego no podía entender: formas modulares, curvas elípticas, grupos de Galois, teoría de Iwasawa, conjetura de Taniyama-Shimura…

Poco a poco, la imagen de lo que había sucedido se iba formando en la red. Andrew Wiles, un matemático británico experto en un campo llamado curvas elípticas, había pronunciado, nada menos que en el Instituto Isaac Newton de Cambridge, tres conferencias en las que, paso a paso, con paciencia y un sentido del arte dramático digno de un Laurence Olivier, avanzó hacia un resultado inevitable.

Durante años, Wiles trabajó en secreto, como un alquimista, sin compartir con nadie ya no digamos sus resultados, ni siquiera la naturaleza de su proyecto. No quería que nadie le quitara la gloria de resolver uno de los problemas más difíciles del mundo matemático. Aunque habían corrido algunos rumores en forma de correos electrónicos, cuando era abordado por algún colega que le preguntaba sobre el contenido de sus conferencias, se limitaba a sonreír y a responder: «Asiste a las conferencias y lo verás».

Tanto secreto espoleó la curiosidad. Así que el auditorio de doscientas personas, formado por avezados especialistas y algunos doctorandos, hervía con cada minuto que pasaba. Al anunciar las conferencias, Wiles tuvo buen cuidado de esconder su proyecto bajo un título aparentemente inocuo. Sin embargo, conforme avanzaba en su exposición, los expertos empezaron a darse cuenta de lo que se cocinaba. Entusiasmados, escribían correos electrónicos en las pausas entre las conferencias, llenos de expectación ante lo que imaginaban que sucedería. Ante el silencio sepulcral de su auditorio, el expositor llenó pizarra tras pizarra de matemáticas complejísimas y novedosas. Finalmente, Wiles escribió unas pocas líneas más que completaban la prueba, hizo una pausa dramática, y garrapateó el enunciado del último teorema de Fermat. Se volvió sonriente hacia el público y dijo: «Creo que voy a dejarlo aquí».

Varias cámaras se dispararon, hubo ovaciones, aplausos… Uno de los problemas más difíciles del mundo, también uno de los más antiguos sin resolver, cayó finalmente ante el ataque sistemático de un matemático brillante que había trabajado a solas durante más de un lustro. Pero ¿cómo es posible? ¿Redescubrió Wiles la prueba de Fermat? No, la historia es mucho más compleja. De hecho, los aplausos resultaron prematuros: la demostración de Wiles contenía un error fatal. Su estrategia de hermetismo tenía ese enorme riesgo: al no compartir sus avances, nadie pudo señalarle ese error antes de que fuera tarde. Y en matemáticas, un solo error, un solo paso en falso, invalida toda la demostración, que se derrumba como un castillo de naipes. Todos los pasos son, precisamente, como esos naipes que apuntalan la estructura de tal forma que, con solo retirar uno de ellos, esta se desmorona. Wiles tuvo por tanto que volver a la pizarra, contrito, y trabajar todavía unos años para dar con una demostración definitiva, a prueba de balas, que finalmente logró publicar en 1994. Pero dejemos por el momento a Wiles, en su máximo momento de gloria, extático ante sus rendidos admiradores.

Es hora de volver a Fermat y enunciar su último teorema. El resultado que el matemático escribió en latín en ese pequeño margen era el siguiente:

Es imposible escribir un cubo como la suma de dos cubos, o una cuarta potencia como la suma de dos cuartas potencias, y en general, para ningún número que sea una potencia mayor que dos ser escrito como la suma de dos potencias del mismo grado.

Escrito en notación algebraica moderna, lo que dice el último teorema es que la ecuación xn+yn = zn, con n>2, no tiene soluciones naturales; es decir, no existen números naturales x, y y z que cumplan la propiedad arriba enunciada: tener un cubo (o potencia mayor) que sea la suma de dos cubos (o potencia mayor del mismo grado).

El teorema de Fermat se aplica exclusivamente a los números naturales (aquellos con los que contamos cosas: 1, 2, 3,… y así indefinidamente); si bien en su enunciado original el autor no dio esta condición explícita, la misma se entiende por contexto.

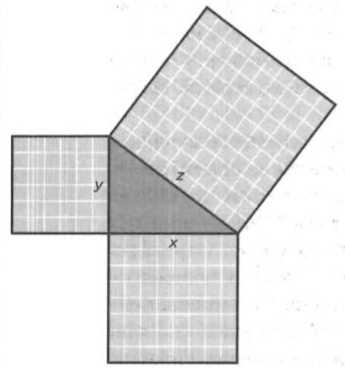
Representación geométrica del teorema de Pitágoras.

Cabe preguntarse por qué Fermat habla solo de exponentes mayores que dos. La respuesta es sencilla. Para el caso n = 1, tenemos un enunciado trivial: en efecto, todo número natural mayor que uno es expresable como la suma de otros dos números (no necesariamente distintos entre sí). Cuando