Martin Gardner - Miscelanea Matematica

MARTIN GARDNER

SALVAT

Compendio de capítulos selectos de las obras Mathematical Camival, Mathematical Magic Show y Mathematical Circus de Martin Gardner.

© 1986. Salvat Editores, S.A. – Barcelona

Mathematical Carnival © 1975. Martin Gardner

Mathematical Magic Show © 1978. Martin Gardner

Mathematical Circus © 1979. Martin Gardner

This translation published by arrangement with Alfred A. Knopf, Inc. and Alianza Editorial, S.A.

ISBN 84-345-8246-5 Obra completa

ISBN 84-345-8415-8

Depósito Legal NA. 844-1986

Publicado por Salvat Editores, S.A. - Mallorca, 41-49 – Barcelona

Impresa por Gráficas Estella. Estella (Navarra)

Printed in Spain

Escaneado: thedoctorwho1967.blogspot.com.ar

Edición digital: Sargont (2017)

Aclaración: Las fórmulas están en formato lineal, para evitar el editor de ecuaciones del Word.

He aquí uno de esos raros y deliciosos acertijos que pueden resolverse en un instante si se atina a enfocarlos correctamente, pero que han sido ideados con sutil ingenio para desviar el pensamiento hacia esquemas equivocados. Se sabe de personas inteligentes que han estado luchando con él más de veinte minutos, para terminar dejándolo por imposible.

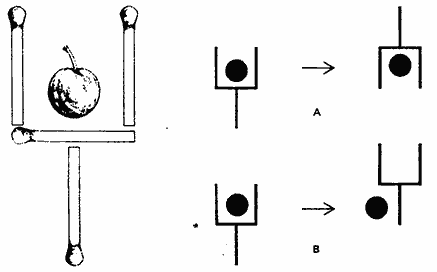
Fig. 1. Un cóctel desconcertante.

Se colocan cuatro cerillas sobre las cuatro dibujadas en forma de copa de cóctel en la figura 1. El problema consiste en mover dos de estas cerillas, y solamente dos, situándolas en nuevas posiciones, con objeto de reconstruir la copa en otro lugar, esta vez con la cereza en el exterior. Es lícito alterar la orientación de la copa, pero la reconstrucción tiene que ser congruente con la dibujada. En la figura 1A vemos cómo mover dos cerillas, dejando la copa boca abajo. Pero el problema no queda así resuelto, pues la guinda sigue dentro de la copa. El dibujo B muestra un procedimiento que sí vacía la copa, pero que no es solución admisible, porque en ella se mueven tres cerillas, y no dos.

¿Cuáles son las dimensiones del mayor de los cubos cuyas seis caras pueden quedar totalmente forradas plegando en torno a él una pieza recortada de una hoja cuadrada de papel, de 3 decímetros de lado? (Como es obvio, la figura recortada en el papel debe ser de una sola pieza.)

Cada uno de los socios del Club V. M. es, o bien veraz, y dirá siempre la verdad al ser preguntado, o bien mentiroso, y entonces responderá siempre una mentira. En mi primera visita al club encontré a todos sus miembros, exclusivamente hombres, sentados en torno a una gran mesa circular, tomando el almuerzo. No había forma de distinguir a veraces de mentirosos por su aspecto externo, así que fui preguntándoles por turno si eran una u otra cosa. De nada me sirvió, pues como era de esperar, todos aseguraron ser veraces. Volví a probar, esta vez, preguntando a cada uno si su vecino de la izquierda era veraz o mentiroso. Para sorpresa mía, todos contestaron que el hombre sentado a su izquierda era mentiroso.

Más tarde, de vuelta a casa, al pasar a máquina mis notas sobre el almuerzo descubrí que había olvidado tomar nota del número de personas sentadas a la mesa. Telefoneé entonces al presidente del club, quien me informó que eran 37. Después de colgar me di cuenta de que no podía confiar en esta cifra, porque no sabía si el presidente era veraz o mentiroso. Decidí, pues, telefonear al secretario del club.

«No, no», me contestó el secretario. «Por desgracia, nuestro presidente es un mentiroso empedernido. La verdad es que estábamos 40 comensales.»

¿A cuál de estos dos hombres debería yo creer? De pronto vi una forma sencilla de resolver la cuestión. ¿Podrá el lector, basándose en la información aquí presentada, determinar cuántos eran los sentados a la mesa? El problema ha sido adaptado de una sugerencia de Werner Joho, un físico de Zurich.

Dos hermanos heredaron un rebaño de ovejas. Las vendieron todas, recibiendo por cada oveja tantos dólares como animales tenía el rebaño. La suma total les fue pagada en billetes de diez dólares, excepto un resto, de menos de 10 dólares, que les fue entregado en dólares de plata. Repartieron entre ambos los billetes de diez, colocando el fajo en medio de la mesa y robando alternativamente de él un billete cada uno, hasta agotarlo.

«¡Pero eso no es justo!», protestó el hermano menor. «¡Tú cogiste el primer billete, y ahora acabas de llevarte el último, así que tienes diez dólares más que yo!»

Para que las partes no fueran tan desiguales, el mayor dio al joven todos los dólares de plata. Pero el hermano pequeño no estaba satisfecho todavía. «Me has dado menos de 10 dólares», arguyó. «Todavía me debes dinero.»

«Es verdad», concedió el mayor. «Supongamos que te hago un cheque de forma que las cantidades con que terminemos ambos sean exactamente iguales. ¿Aceptarías?»

Y así se hizo. ¿Por qué valor fue extendido el cheque? Aunque la información suministrada parezca insuficiente, es posible responder a la cuestión.

Ronald A. Wohl, que es químico en la Universidad de Rutgers, me hizo saber recientemente de este precioso problema, que había descubierto en un libro francés. Posteriormente descubrí en mi archivo una carta de Carl J. Coe, matemático jubilado de la Universidad de Michigan, donde analizaba un problema esencialmente idéntico que, según me dijo, había estado rodando entre sus colegas allá por los años cincuenta. Tengo la impresión de que el problema sigue siendo poco conocido todavía.

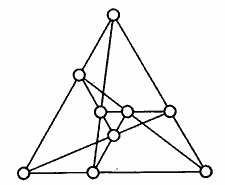
El tablero sobre el que se juega el tatetí (o «tres en raya») puede considerarse como formado por nueve casillas dispuestas en ocho líneas de tres casillas cada una. Empero, nueve casillas pueden sin dificultad disponerse en nueve, o incluso diez, líneas de tres. Thomas O’Beirne, de Glasgow, autor de Puzzles and Paradoxes (Oxford, 1965) ha estado experimentando con configuraciones de nueve líneas, topológicamente distintas, para ver si algunas se prestaban al juego de tres en raya, y descubrió que el primer jugador podía ganar con una estrategia trivial en todas las configuraciones regulares, a excepción de la mostrada en la figura 2

.

Fig. 2. El juego de Tri-Ex.

Para jugar al Tri-Ex (nombre con que O’Beirne ha bautizado a su juego) cada jugador necesita cuatro monedas. Para distinguirlas, uno puede usar pesetas, y otro, duros. Al primer jugador no se le permite llegar a la quinta jugada. Los adversarios van colocando por turno una moneda en alguno de los círculos vacíos; el primero en conseguir «meter en raya» tres de sus monedas gana. Suponiendo que ambos desarrollen un juego óptimo, ¿habrá una estrategia vencedora —sea para el primero, sea para el segundo— o lo más que podrá conseguirse es empatar, como sucede en el tatetí ordinario?

El papel que desempeñan configuraciones como ésta en la geometría moderna ha sido analizado con mucha amenidad por Harold L. Dorwart en The Geometry of Incidence (Prentice-Hall, 1966), así como en el librito de instrucciones de un rompecabezas inventado por él, Configurations, comercializado por los fabricantes del juego lógico WFF’N PROOF. Además de sus propiedades topológicas y combinatorias, la disposición aquí mostrada tiene una estructura métrica poco habitual. En cada una de las alineaciones de tres puntos, el central corresponde a la sección áurea del segmento definido por los puntos extremos.