Chris McMullen - Una introducción visual a la Cuarta Dimensión

Una introducción visual a la

(geometría rectangular 4D)

Chris McMullen, PH.D

Northwestern State University

de Luisiana

Enero de 2013

Versión en español: Sargont (2019)

Contenido

Introducción

Este libro proporciona una introducción visual y c o l o r i d a a la cuarta dimensión. Pero no es sólo un libro ilustrado. Encontrarás explicaciones claras que te ayudarán a entender los conceptos, y un toque de personalidad (¡con unos cuantos monos!) haciendo una lectura atractiva en lugar de un texto matemático seco. El contenido es muy accesible , ya que no se necesita tener una formación sólida en matemáticas para entenderlo, pero los conceptos son lo suficientemente avanzados y detallados como para satisfacer la curiosidad de un lector que se destaca en matemáticas. Este libro se centra puramente en los aspectos geométricos de la cuarta dimensión; no hay ningún componente espiritual o religioso en este libro. Los objetos geométricos considerados en este libro son rectangulares; el principal objeto 4D discutido es el teseracto (un hipercubo 4D), y está descrito con gran detalle y acompañado de muchas imágenes instructivas. ¡Que disfruten su viaje a la cuarta dimensión!

Capítulo 0

¿Qué es una dimensión?

A ntes de empezar, aclaremos lo que queremos decir con una dimensión. Como definición simple, una dimensión es una medida de la extensión . Las dimensiones de un objeto -no, no un simple objeto viejo, sino un mono con piel de color A R C O I R I S , así que esto no se leerá como un aburrido libro de matemáticas- se refieren a las diferentes direcciones en las que se extiende un objeto. El mono tiene altura (qué tan alta es, por supuesto que es una niña, ¿qué más podría ser?), anchura (qué tan ancha es, hombro con hombro) y profundidad (de adelante hacia atrás, o de la nariz hasta la cola); es tridimensional (3D).

Sin embargo, hay diferentes tipos de dimensiones, como el espacio y el tiempo - o si quieres ser exótico, podemos hablar de la dimensionalidad de tus pensamientos o incluso de tu olor corporal. Necesitamos explorar el concepto de una dimensión un poco más allá, para que sepas exactamente qué tipo de dimensiones estamos discutiendo en este libro.

Comencemos con un simple ejemplo geométrico. Un punto infinitesimal tiene dimensiones cero (0D) - no se extiende en ninguna dirección. (Sí, infinitesimal. ¿Te gusta esa palabra? Seguramente conoces la palabra infinito - el número más grande, ¿verdad? ¡Equivocado! Si fuera un número, podría agregarle uno y encontrar un número mayor. El infinito representa el concepto de que puedes seguir contando para siempre. Infinitesimal sería el número más pequeño que no es cero, excepto que si lo divides por dos, obtienes algo más pequeño. Así que esta definición es tan errónea como pensar en el infinito como en ser el número más grande. Pero a veces una definición incorrecta expresa el concepto más claramente que una técnicamente correcta.) Esa larga observación parentética en realidad tiene un propósito. ¿Decir qué? Sí: Pasamos mucho tiempo sin llegar a ninguna parte, ¡igual que la dimensión cero! Una línea es unidimensional (1D) ya que sólo se extiende en una dirección, como esta frase, que sólo se puede leer hacia adelante o hacia atrás. Un plano es bidimensional (2D); tiene longitud y anchura. Un bloque es tridimensional (3D); tiene longitud, anchura y profundidad.

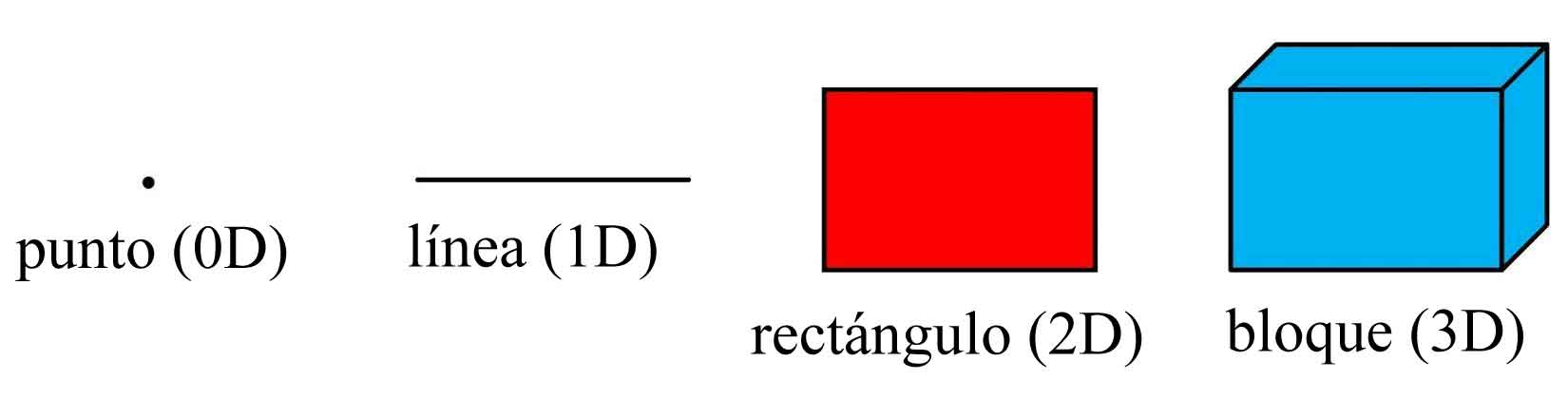
Si quieres que la imagen anterior parezca menos aburrida, tienes que usar tu cerebro e imaginar que consiste en -de izquierda a derecha- el pensamiento de un mono, la cola de un mono, la sombra de un mono y un mono. (Claro, el autor podría haber dibujado monos, pero eso le privaría de la oportunidad de imaginar sus propios monos. En realidad, la verdadera razón es que vamos a dibujar objetos 4D, y probablemente serán mucho más fáciles de entender si se parecen más a rectángulos y menos a monos. Seguiremos hablando de monos, sin embargo, para darle más sabor al texto, pero los dibujos serán sencillos, aburridos y en línea recta. Sólo recuerda que todas esas líneas rectas son realmente colas de mono. Tenga cuidado de no pincharlas con el dedo al dar vuelta la página. Gracias.)

Nuestro universo parece ser tridimensional porque sólo podemos (oops, que debería decir “los monos pueden”) movernos en tres direcciones independientes: norte/sur, este/oeste, y arriba/abajo. Cualquier otra dirección es una combinación de estas. Por ejemplo, cuando un mono lanza un coco al noreste, el coco se mueve esencialmente al norte y al este al mismo tiempo.

Por eso pensamos que el espacio es 3D. ¿Qué es? Mira, intenta que un mono se mueva en alguna dirección que no sea una combinación de adelante/atrás, izquierda/derecha y arriba/abajo. Buena suerte con eso. Cuando seas capaz de hacerlo y demostrar que lo has hecho, tendrás un Premio Nobel (eso es “sin campana”, no “noble”; además, será en física, no un premio de la Paz).

El espacio parece ser 3D, pero el espacio-tiempo es 4D. El tiempo es una dimensión en el sentido de que es también una medida de la extensión -es una duración. (Las patas del sofá no están haciendo nada ―doble negativo; sí, sé que puedo cancelar los signos menos―. La actividad es 0D con respecto al espacio, pero están haciendo tiempo. ¡Todo ese tiempo que pasamos esperando en las filas y el tráfico cuenta para algo!) Pero el tiempo es claramente un tipo diferente de dimensión que la longitud, el ancho y la profundidad.

En este libro, nos interesa una cuarta dimensión del espacio. Es decir, una cuarta dimensión que es muy parecida a la longitud, anchura y profundidad, pero no una combinación de éstas (es decir, no como el noreste).

La teoría de las cuerdas en realidad predice que nuestro universo tiene más que tres dimensiones del espacio. Nuestro universo podría tener 9 dimensiones de espacio. (Eso hace 10 dimensiones del espacio-tiempo. Si oíste que son 11, estás pensando en la teoría M. Tal vez pensaste que era 26; entonces déjame corregirme y decir que la teoría moderna de las supercuerdas predice 9, mientras que la teoría de cuerdas original tenía 25 ―agrega tiempo para hacer veintiséis―.) ¿Pero quién está contando? De cualquier manera, sólo percibimos 3.

¿Cómo es posible que la teoría de cuerdas sea correcta? ¿Cómo puede alguien creer una teoría que dice que hay nueve dimensiones del espacio, cuando es bastante obvio que sólo hay tres?

Las otras seis dimensiones pueden estar ocultas . Pueden ser dimensiones muy pequeñas que se envuelven en círculos. Por ejemplo, las tres dimensiones que percibimos pueden ser como la longitud del cilindro ilustrado a continuación, mientras que las dimensiones adicionales pueden ser como la circunferencia. La circunferencia es pequeña, mientras que la longitud es infinita. Si las dimensiones extras son muy pequeñas, eso explicaría por qué no puedes verlas y por qué no puedes moverte a lo largo de una cuarta dimensión.