Singer - Una práctica teoría de la optimización lineal : datos, modelos y decisiones

Agradecimientos

Mucha gente ha colaborado con este libro pero sólo yo aparezco como autor. En estas líneas espero hacer algo de justicia.

Primero, tengo que mencionar a mis colegas Bárbara Prieto, Francisco Poblete y Christian Villalobos, junto a quienes por varios años he dictado el curso de “Métodos de Optimización” en la Escuela de Administración de la Pontificia Universidad Católica de Chile. También a los ayudantes del ramo, que son demasiados como para mencionarlos. Cada semestre intentamos plantear en pruebas y controles problemas novedosos y atingentes a la realidad. Los problemas que creo son los más interesantes los he seleccionado y, cuando he podido, los he enriquecido. Aprecio el trabajo en equipo que hemos llevado a cabo todos estos años, cuyo resultado está contenido en este texto.

También han contribuido los alumnos que han tomado el curso de “Métodos”. Todos ellos son importantes, especialmente quienes más dificultades tuvieron, pues en ellos mi trabajo pudo tener más impacto. A muchos les fallé pues no logré dejarles un buen recuerdo. No fue por falta de interés ni de esfuerzo; fue sólo falta de talento.

Muchas de las aplicaciones hacen referencia a trabajos de consultoría que hemos realizado en conjunto con mi querido amigo Patricio Donoso y, más recientemente, con Pedro Traverso, Garo Konstantinidis y Francisco Brahm, y otros profesionales y miembros de CEOP Consulting. Extiendo mi agradecimiento a mis colegas y amigos de la Escuela de Administración, de quienes siempre he recibido apoyo y afecto.

Agradezco a Ediciones UC por su apoyo y a la diseñadora María Eugenia Pino por su trabajo. Muy especialmente le doy las gracias a Gimena Pardo por toda la ayuda que me ha brindado en éste y muchos otros proyectos profesionales.

También quiero mencionar a mi familia, en especial a mi madre Dolores González, que siempre me ha dado todo y mucho más de lo que he necesitado.

Concluyo mis palabras de agradecimiento hacia quien más le debo: mi señora, María Inés Olivares (Mané). Ella es mi mayor motivación para ser una persona de bien. Le dedico este libro porque ha inspirado mi vida y por haberme regalado a mis tres hijos. Espero cumplir, aunque sea sólo en parte, con la tarea a la que nos hemos encomendado: motivar y ayudar a mis alumnos a comprender el mundo en el que vivimos para que ellos, cuando sea su momento, aporten lo que les corresponde.

A mi amada esposa Mané

y a mis tres hijos Eitán, Igal y Noam,

quienes son la luz de mi vida.

Prefacio

Las Ciencias Cuantitativas de la Administración

Albert Einstein (1879-1955) escribió: “D’ios no juega a los dados sino más bien ha dictado leyes según las cuales la realidad se desarrolla. El afán de la ciencia es descubrir estos pensamientos de D’ios”. Lo más probable es que el desempeño de las empresas y las organizaciones tampoco sea fruto de un juego de dados, sino de un sinnúmero de decisiones. Cuanto mayor sea la comprensión de las leyes que rigen su realidad, más acertadas serán sus decisiones.

La ciencia intenta descubrir las leyes de la realidad conjeturando modelos para luego, a la luz de la evidencia, validarlos o descartarlos. Un modelo es una descripción simplificada de un fenómeno, donde la relación entre sus principales conceptos (por ejemplo, la causalidad) está descrita de manera formal. Según Galileo Galilei (1564-1642), las leyes de la realidad se revelan (y describen) en el lenguaje de las matemáticas. Por ello, hasta el Siglo XVI la descripción de la trayectoria de los planetas fue siempre problemática: Marte, Júpiter y Saturno parecían detenerse en el cielo nocturno y comenzaban a moverse en sentido contrario. La astronomía Ptolemaica, que se valía de la geometría para describir la mecánica celeste, conjeturaba que tales planetas viajaban en dos órbitas alrededor de la Tierra: una principal ( deferente ) y otra secundaria ( epiciclo ). Sin embargo, se necesitaban demasiados epiciclos diferentes para ajustar los datos al modelo, lo cual lo hacía complicado, arbitrario y, por ende, poco plausible.

Para descifrar el acertijo, Nicolás Copérnico, pudo explicar la trayectoria de los planetas y otras observaciones astronómicas de manera simple y por lo tanto más verosímil.

Una teoría relacionadas con la dirección de las organizaciones. Surgió durante la Segunda Guerra Mundial como resultado del rol que tuvo el mundo científico en la conducción del Ejército Aliado. Mientras Adolf Hitler se asesoraba por adivinos y astrólogos, Winston Churchill y Franklin D. Roosevelt se rodearon de los mejores científicos de la época. El primer encargo del que se tiene registro es la solicitud que Churchill le hizo a Patrick Blackett –quien ganaría el Premio Nobel de Física en 1948– de evaluar la conveniencia de entregar apoyo aéreo a la campaña rusa en Alemania (Blackett, 1948). El beneficio que éste y otros estudios le depararon al Ejército Aliado le acarreó a las ciencias cuantitativas de la administración la credibilidad necesaria para influir en la toma de decisiones. Al terminar la Guerra, muchos de los asesores científicos se abocaron al estudio teórico de los modelos matemáticos y a su aplicación a los problemas de las empresas e instituciones (Dantzig, 2002).

El rol de los modelos cuantitativos en la toma de decisiones puede entenderse mediante la Ilustración A. El modelo sirve de “archivo” que le da coherencia y significado a los datos que describen los fenómenos (Friedman, 1953). De los modelos las personas extraen conceptos, es decir ideas comprensibles, que les sirven para tomar decisiones (Pidd, 1999).

Ilustración A : Datos, modelos y decisiones

La administración de empresas también se revela en el lenguaje de las matemáticas. Consideremos el problema de una tienda que debe determinar el nivel de inventario óptimo, lo que equivale a definir el tamaño Q de la orden de productos solicitada a sus proveedores. Tal como lo muestra la Ilustración B, la descripción del problema pasa por sucesivos niveles de abstracción. Un primer nivel es la descripción verbal. Ésta debe ser precisa y concisa, y debe diferenciar cuáles elementos son esenciales y cuáles no. Un siguiente nivel de abstracción es la representación gráfica, que muestra el comportamiento del inventario mediante un diagrama. El nivel algebraico traduce la descripción gráfica a expresiones matemáticas, susceptibles de ser manipuladas por el cálculo o cualquier otro instrumento lógico-matemático.

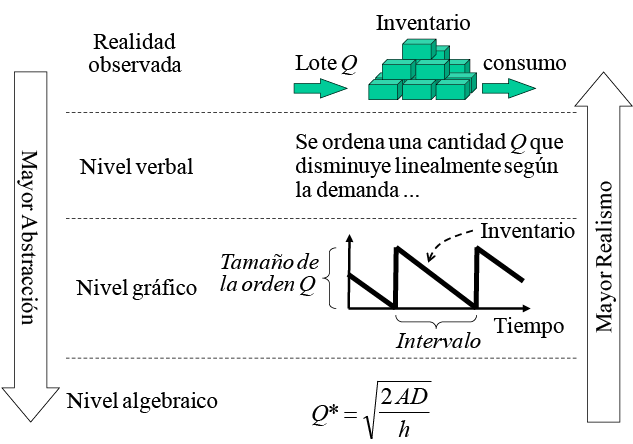
Ilustración B: Niveles de abstracción de la planificación de inventarios

Mientras más abstracta es la descripción, mayor es su capacidad de deducir conclusiones. En la Ilustración B el álgebra permite utilizar la condición de primer orden –derivar e igualar a cero la función de costo– para deducir la cantidad óptima Q * a ordenar. Este nuevo conocimiento es interpretado y aplicado a niveles de menor abstracción y de mayor realismo; en definitiva, a la realidad concreta (Greenberg, 1993).

La Programación Lineal

Un método para razonar por abstracción-deducción-interpretación es identificar los parámetros icionan el valor que pueden tomar las variables. En resumen, la función objetivo expresa lo que se quiere hacer; las restricciones expresan lo que se puede hacer.

Los modelos de optimización de una función objetivo sujeta a un conjunto de restricciones se denominan de programación matemática .

El desarrollo de la programación lineal significó un progreso sin precedentes en la administración de empresas. Un ejemplo en el que trabajó Dantzig consistía en asignar 70 personas a 70 actividades. No obstante es un problema relativamente pequeño en la práctica, el número de posibles soluciones es 70! (factorial), mayor que 10. Si una computadora pudiera calcular mil millones de asignaciones por segundo, no podría resolver este problema aunque hubiera empezado a trabajar cuando se creó el universo. El método Simplex simplifica la enorme complejidad computacional, resolviendo esta asignación de 70 × 70 en pocas iteraciones que un microcomputador calcula casi instantáneamente. El trabajo posterior de Dantzig inauguró la optimización a gran escala, la programación lineal estocástica y otras áreas de investigación que tuvieron un profundo impacto en muchas disciplinas científicas (Orden, 1993).