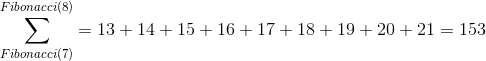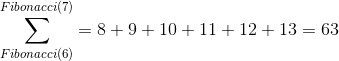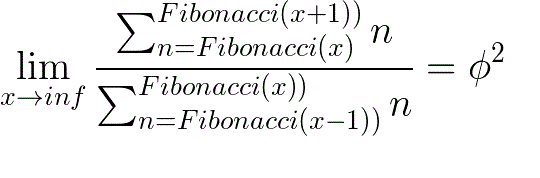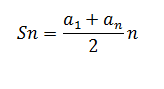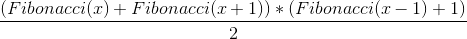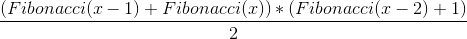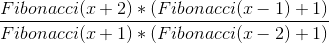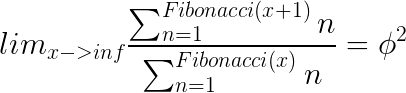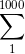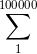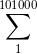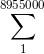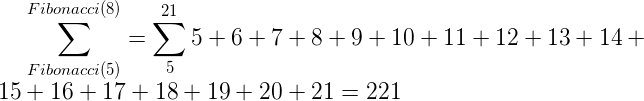Pedro Hugo García Peláez - Series e Integrales Logarítmicas de Fibonacci

Series e Integrales Logarítmicas de Fibonacci Pedro Hugo García Peláez Reservados todos los derechos. No se permite la reproducción total o parcial de esta obra, ni su incorporación a un sistema informático, ni su transmisión en cualquier forma o por cualquier medio (electrónico, mecánico, fotocopia, grabación u otros) sin autorización previa y por escrito de los titulares del copyright. La infracción de dichos derechos puede constituir un delito contra la propiedad intelectual. © Pedro Hugo García Peláez, 2019 Prólogo

Aunque las demostraciones y ecuaciones sin ser difíciles, son un poco tediosas de leer, por eso espero que después de hacer un pequeño esfuerzo tengas tu recompensa al final con las espirales logarítmicas que podrás ver y crear tu mismo. La suma de todos los números desde Fibonacci(n-1) hasta Fibonacci(n) tiene dos propiedades. Si sumamos todos los números naturales desde Fibonacci(n-1) hasta Fibonacci(n).

Por ejemplo la suma entre 13 y 21 es: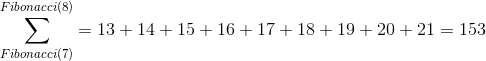
La suma inmediatamente inferior sera la suma de todos los naturales entre los dos números de Fibonacci anteriores.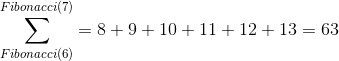
Podemos ver que el cociente se acerca a Phi al cuadrado. En este caso 153/63 = 2.428 vemos que se acerca algo al número Phi² = 2.618... La expresión matemática de esta relación es:

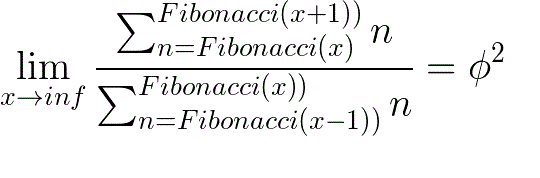
Y la prueba es bastante fácil Usando la fórmula de una suma aritmética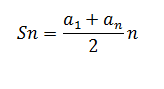

Vemos que (a1) es Fibonacci(x) (an) es Fibonacci (x+1) y (n) que es el número total de de términos es Fibonacci (x-1) al que hay que sumarle 1 ya que el número total de términos es: n = Fibonacci(x+1) – Fibonacci (x) +1 = Fibonacci(x-1) + 1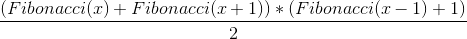

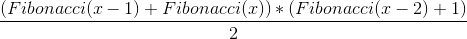
Simplificando ambos 2 y por las propiedades de los números de Fibonacci Fibonacci(x)+Fibonacci(x+1) = Fibonacci(x+2) Fibonacci(x-1)+Fibonacci(x) = Fibonacci(x+1) Por lo que tenemos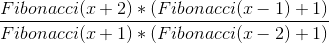
El primer término tiende a Phi y el segundo también tiende a Phi aunque se le sume una unidad a cada término para números de Fibonacci que tiendan a infinito esa unidad es despreciable, y por otra parte esa unidad va a ser fundamental para demostrar la siguiente propiedad. La relación también funciona para sumas cuyo primer término sea 1 y el último un número de Fibonacci cualquiera. O sea: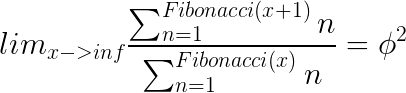
Obviamente esto también debería funcionar usando integrales y de hecho funciona de una forma exacta sin la pequeña desviación cuando usamos sumas.

Aunque es una conjetura creo que se puede generalizar para todo tipo de series cuyos números de términos sean la suma de los dos anteriores. Me parece que se puede generalizar del mismo modo que cualquier sucesión de Fibonaci sean los que sean sus do primeros números tiende a Phi. En este caso el cociente de estos término tenderá a Phi^2 sean los que sean sus números iniciales y cuya única condición es que el incremento de términos sea la suma de los dos anteriores. Lo podemos ver con un ejemplo: Vamos a hacer un sucesión de series empezando todas por el número 1 aunque se podría poner cualquier número es más fácil de operar y visualizar así. E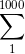
l primer término sería: El segundo: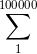
El tercero tendría un número de término igual a la suma de estos dos osea: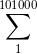
El siguiente término sería la serie que va desde 1 a 201000 y así sucesivamente Sólo voy a hallar la suma para los términos 12 y 13 La serie que ocupa el lugar doce es igual a: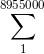
Que vale: 40096016977500 La serie que ocupa el lugar treceavo es: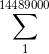
Cuya suma es: 104965567744500 El cociente entre ambos es: 104965567744500/40096016977500 = 2.617855229944... Pero acaba de empezar la muestra de lo mucho que sale el número Phi^2 en la sucesiones ahora vamos a ver una propiedad muy curiosa.

Supongamos que tenemos cualquier serie de números naturales por ejemplo una que empieza en 3660 y tiene 2330 términos o sea sería 3660+3661......+5988+5989 El resultado de sumar la serie nos da 11241085 y la media aritmética de la serie es: 4825,5 si multiplicamos este número por dos nos da 9646 y si construimos otra serie empezando por el último número de la serie y como último término de la sucesión esta media que hemos multiplicado por dos tenemos la siguiente serie: 5989+5990+......+9645+9646 Cuya suma nos da. 285596415 y cuya media es 285596415/3658 = 7817.5 Puedes comprobar que el cociente entre las dos medias de las sucesiones hallado tiende a Phi 7817.5/4825.5= 1.62 Si tienes una sucesión de números naturales y quieres hallar la siguiente que esté con una relación igual a Phi ya sabes lo que tienes que hacer. Pero la relación más sorprendente es la de los números de Fibonacci y los logaritmos Neperianos. Para ello vamos a definir otra sucesión entre números de Fibonacci cuya posición sea a su vez un índice de Fibonacci. O sea un término de esta serie sería.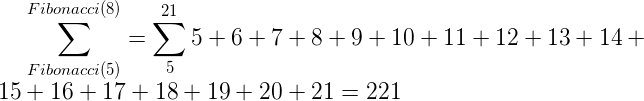
El siguiente término de la sucesión sería:


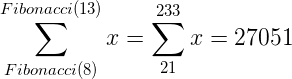
En resumen los primeros términos de esta sucesión son: Fibonacci(Fibonacci(1)) = 1 = Fibonacci(1) Fibonacci(Fibonacci(2)) = 1 = Fibonacci(1) Fibonacci(Fibonacci(3)) = 1 = Fibonacci(2) Fibonacci(Fibonacci(4)) = 2 = Fibonacci(3) Fibonacci(Fibonacci(5)) = 5 = Fibonacci(5) Fibonacci(Fibonacci(6)) = 21 = Fibonacci(8) Fibonacci(Fibonacci(7)) = 233 = Fibonacci(13) Fibonacci(Fibonacci(8)) = 10946 = Fibonacci(21) Fibonacci(Fibonacci(9)) = 5702887 = Fibonacci(34) Hay que observar que: Fibonacci(Fibonacci(x) + Fibonacci(Fibonacci(x+1) ≠ Fibonacci(Fibonacci(x+2) Sin embargo a causa de las propiedades de los números de Fibonacci.