Ian Stewart - Números increíbles

El cero surgió primero en sistemas para escribir los números. Era un recurso de notación. Solo más tarde fue reconocido como un número por derecho propio y se le permitió ocupar su lugar como una característica fundamental de los sistemas numéricos matemáticos. Sin embargo, tiene muchas características inusuales y, a veces, paradójicas. En particular, no resulta razonable dividir entre cero. En los cimientos de las matemáticas, todos los números pueden derivarse a partir de 0.

En muchas culturas antiguas, los símbolos para 1, 10 y 100 no estaban relacionados. En la Grecia antigua, por ejemplo, usaban letras de su alfabeto para denotar los números 1-9, 10-90 y 100-900. Esto resulta potencialmente confuso, aunque normalmente es fácil decidir si el símbolo hace referencia a una letra o a un número a partir del contexto. Pero también complica la aritmética.

El modo en que escribimos números, con el mismo dígito representando números diferentes dependiendo de dónde está, se llama «notación posicional» [véase 10]. Este sistema tiene ventajas importantes para la aritmética de papel y lápiz, que hasta hace poco era como se hacían la mayoría de las operaciones del mundo. Con la notación posicional, lo principal que necesitas saber son reglas básicas para sumar y multiplicar los diez símbolos 0 – 9. Hay patrones comunes cuando los mismos símbolos aparecen en lugares diferentes. Por ejemplo:

23 + 5 = 28

230 + 50 = 280

2.300 + 500 = 2.800

Figura 66

No obstante, usando la antigua notación griega, las dos primeras tienen el siguiente aspecto

κγ + ε = κη

σλ + ν = σπ

sin una estructura común obvia.

Sin embargo, hay una característica extra de la notación posicional, la cual aparece en 2.015: la necesidad de un símbolo cero. En este caso nos indica que no hay centenas involucradas. La notación griega no necesita hacer eso. En σπ , por ejemplo, σ significa 200 y π significa 80. Podemos decir que no hay unidades porque no aparece ninguno de los símbolos de las unidades: α – θ . En lugar de usar el símbolo cero, simplemente evitamos escribir cualquiera de los símbolos de las unidades.

Si intentamos hacer esto en el sistema decimal, 2.015 se convierte en 215, pero no podemos decir si significa 215, 2.150, 2.105, 2.015 o, es más, 2.000.150. Versiones iniciales de la notación posicional usaban un espacio 2 15, pero no es fácil darse cuenta de que hay un espacio, y dos espacios juntos son un espacio ligeramente más largo. De modo que es confuso y resulta fácil cometer un error.

Babilonia

La primera cultura que introdujo un símbolo con el significado de «ningún número aquí» fue la babilónica. Recuerda [véase 10] que la notación numérica babilónica no usaba base 10, sino base 60. La primera aritmética de Babilonia indicaba la ausencia de un término 602 con un espacio, pero alrededor de 300 a. C. ya habían inventado un símbolo especial 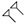. Sin embargo, parece que en Babilonia no habían pensado en este símbolo como un número por derecho propio. Además, lo omitían si estaba al final del número, de modo que el significado tenía que sacarse a partir del contexto.

India

La idea de la notación posicional de base 10 aparece en Lokavibhâga, un texto sobre cosmología del jainismo que data de 458 d. C., el cual también usa shunya (que significa «vacío»), donde nosotros usaríamos 0. En 498 d. C., el famoso matemático y astrónomo hindú Aryabhata describió la notación posicional como «posición a posición incrementa 10 veces su valor». El primer uso no controvertido de un símbolo específico para el dígito decimal 0 aparece en el año 876 d. C. en una inscripción en el templo Chaturbhuja, Gwalior, y adivina qué: es un círculo pequeño.

Los mayas

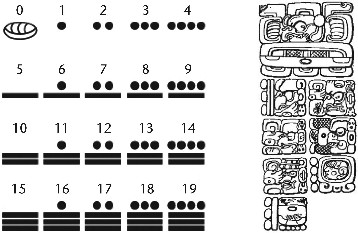
La civilización maya de América Central, la cual alcanzó su esplendor entre los años 250 y 900 d. C., empleó una notación de base 20 y tenía un símbolo explícito para cero. Este método se remonta a mucho antes y se cree que fue inventado por los olmecas (1500-400 a. C.). Los mayas hicieron un uso considerable de los números en su sistema de calendario, un aspecto del cual se conoce como «la Cuenta Larga». Este asigna una fecha a cada día contando cuántos días han pasado desde una fecha de creación mítica, que sería el 11 de agosto de 3114 a. C. en el actual calendario occidental. En este sistema un símbolo para cero es esencial para evitar la ambigüedad.

Figura 67. Izquierda: números mayas. Derecha: una estela en Quirigua en la que aparece la fecha de la creación maya: 13 baktun, 0 katun, 0 tun, 0 uinal, 0 kin, 4 Ahau 8 Cumku. Esto equivale a nuestro 11 de agosto de 3114 a.C.

Antes del siglo IX d. C., el cero era visto como un símbolo práctico para los cálculos numéricos, pero no se le consideraba un número como tal. Probablemente, porque no contaba nada.

Si alguien te pregunta cuántas vacas tienes y las tienes, las señalas de una en una y cuentas «una, dos, tres...». Pero si no tienes vacas, no señalas una y dices «cero», pues no hay ninguna vaca que señalar. Como no puedes obtener 0 contando, no resulta evidente que sea un número.

Si esta actitud parece extraña, merece la pena observar que, hace más tiempo todavía, no se pensaba en «uno» como un número. Si tienes vacas, seguramente tengas más de una. Una distinción parecida puede todavía encontrarse en el lenguaje moderno: la diferencia entre singular y plural. En la Grecia antigua también tenían una forma «dual», con modificaciones específicas de palabras usadas cuando hablaban de dos objetos. De modo que en ese sentido «dos» no se consideraba un número como el resto. Otras cuantas lenguas clásicas hacían lo mismo, y algunas de las modernas, como el escocés, el galés y el esloveno todavía lo hacen. Quedan algunos rastros en el español como «ambos» para dos cosas, pero «todo» para más.

A medida que se extendió el uso del cero como un símbolo y los números se empleaban para otros propósitos distintos que contar, se hizo evidente que en la mayoría de los aspectos el cero se comporta como cualquier otro número. En el siglo IX , los matemáticos hindúes consideraban cero un número como cualquier otro, no solo un símbolo usado como separación de otros símbolos para que quedase más claro. Usaban el cero sin reservas en sus operaciones diarias.

En la imagen de la recta numérica, en la que los números 1, 2, 3, ... están escritos en orden de izquierda a derecha, está claro dónde debe ir 0: inmediatamente a la izquierda de 1. La razón es sencilla: sumando 1 a cualquier número se mueve un paso hacia la derecha. Sumando 1 a 0 se mueve a 1, de modo que 0 tiene que ir en el lugar en el que un paso a la derecha dé como resultado 1. Y esto es un paso a la izquierda de 1.

La aceptación de números negativos determinó el lugar del cero como un número verdadero. Todo el mundo estaba contento con 3 siendo un número. Si aceptas que –3 también es un número y que siempre que sumas dos números obtienes un número, entonces 3 + (–3) tiene que ser un número. Y este número es 0.