HUGO STEINHAUS
INSTANTANEAS
MATEMATICAS
SALVAT
Versión española de la tercera edición de la obra norteamericana Mathematical snapshots publicada por Oxford University Press, Inc. de Nueva York
Traducción: Luis Bou García
Escaneado y Edición digital: Sargont (2018)
© 1987. Salvat Editores, S.A. – Barcelona
© Oxford University Press, Inc. - New York
ISBN 0-19-503267-5 Edición original
ISBN 84-345-8246-5 Obra completa
ISBN 84-345-8428-X
Depósito legal NA-1153-1986
Publicada por Salvat Editores, S.A. - Mallorca, 47 - 08029 Barcelona
Impreso por Gráficas Estella, S.A. Estella (Navarra)-1987
Printed in Spain
Índice de capítulos
(Los números corresponden a las ilustraciones o al texto que las acompaña.)
Prólogo
Sea más que bienvenida esta nueva y tercera edición, ampliada, de las Instantáneas Matemáticas de Steinhaus.
Es preciso no confundir este libro con las numerosas obras de divertimentos, rompecabezas y paradojas. Aunque tales libros puedan ser amenos, su contenido matemático acostumbra a ser de escasa importancia, cuando no trivial. Muchos, por ejemplo, presentan demostraciones falsas, y se desafía al lector a descubrir las falacias.
El profesor Steinhaus no se ocupa de tales pasatiempos. Sus «instantáneas» se refieren a fragmentos seleccionados, espigados de entre las diversas partes de la matemática elemental. Estos fragmentos tocan temas plenamente matemáticos, que no es corriente encontrar ni en los textos ni en los libros de carácter popular. Muchos tienen aplicación a problemas reales, y Steinhaus presenta tales aplicaciones. El gran mérito de los temas que ha elegido es que, sobre ser deliciosos, nos dejan atónitos e intrigados. Grande es la diversidad de sus temas. Contiene construcciones geométricas infrecuentes, juegos plenos de contenido matemático, lúcidos razonamientos sobre triángulos, cuadrados, poliedros y círculos, así como otros aspectos muy novedosos. Todos ellos son independientes, por lo que cada cual puede concentrarse en los que le atraigan más. Todos interesan, y, muchas veces, apasionan.
El profesor Steinhaus explica las matemáticas, y sus espléndidas figuras y excelentes fotografías son de inmensa utilidad para la comprensión de lo que nos ha mostrado. No deja Steinhaus de plantearnos cuestiones, cuyas respuestas están muchas veces al alcance de casi todos los lectores; pero es preciso advertir al lector de que la solución de algunas de ellas ha resistido hasta la fecha los esfuerzos de los más grandes matemáticos. La demostración matemática requiere más que la pura intuición, que inferencia a partir de casos particulares, o que evidencia visual.
El libro debe —y puede— ser leído por profanos interesados en conocer las sorpresas que la matemática elemental es capaz de ofrecernos. El profesor Steinhaus es un matemático muy distinguido, y, como demuestra el hecho de haber emprendido la presentación de ciertos rasgos insólitos, aunque elementales, de las matemáticas, está seriamente interesado en la difusión del conocimiento y pensamiento matemáticos. El atento lector podrá, al tiempo que disfruta con el material que le es presentado, aprender sólidas nociones matemáticas, lo cual reviste hoy tanta importancia como en 1938, fecha de la primera edición polaca de este libro.
M ORRIS K LINE
Professor Emeritus de Matemáticas
del Instituto Courant de Ciencias Matemáticas.
Universidad de Nueva York
Prefacio
Quisiera, al presentar este libro al lector, poder evitar el riesgo de ser mal entendido, riesgo que todo matemático corre al dirigirse al público no especializado. No tengo el propósito de enseñar (en el sentido habitual del término) ni de divertir, al lector con unas cuantas charadas. Lo que ocurre es que durante un precioso día de verano me hicieron esta pregunta: «Afirma usted ser matemático. Bueno, ¿y, cuando se es matemático, a qué se dedica uno todo el día?». Estábamos, mi interlocutor y yo, sentados en un parque, y me esforcé en explicarle unos cuantos problemas geométricos, resueltos unos, y otros no, ayudándome de un palito para trazar en el albero una curva de Jordán, una curva de Peano... Así fue como se concibió este libro, en el cual los dibujos, diagramas y fotografías facilitan un lenguaje directo y permiten evitar las demostraciones, o, al menos, reducirlas a un mínimo.
H. S TEINHAUS
1. Triángulos, cuadrados y juegos
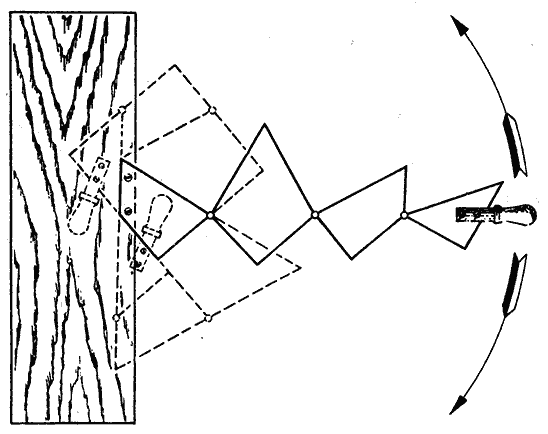
| Fig. 1 |
Con estas cuatro pequeñas piezas planas (1) podemos componer un cuadrado o un triángulo equilátero, según llevemos el mango hacia arriba o hacia abajo. La demostración viene dada mediante un dibujo (2).
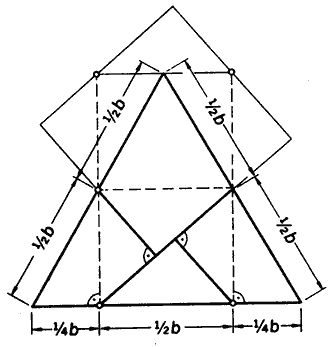
| Fig. 2 |
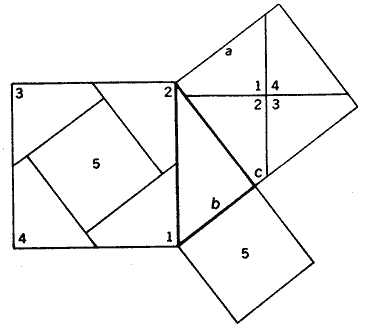
| Fig. 3 |
Para descomponer un cuadrado en dos cuadrados trazamos un triángulo rectángulo (3) ; para comprobar que el cuadrado grande es la suma de los otros dos, descomponemos en cuatro piezas el cuadrado mediano, trazando por su centro una recta vertical y otra horizontal, y desplazamos después estas cuatro piezas (por traslación, sin hacerlas girar) llevándolas a ocupar los cuatro vértices del cuadrado grande; la porción de cuadrado no recubierta tiene exactamente el mismo tamaño que el cuadrado pequeño. Para comprobarlo, no tenemos más que observar que a = b + c. El significado del teorema así demostrado salta a la vista en cuanto nos fijamos en el triángulo (4) de lados 3, 4 y 5 → 9 + 16 = 25. Así pues, podemos trazar un ángulo recto valiéndonos de una cuerda de 1,20 m de longitud, en la que se han hecho nudos separados 3, 4 y 5 dm.
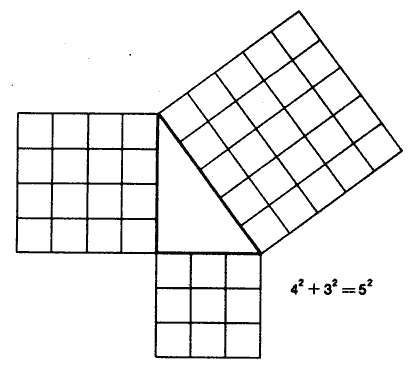
| Fig. 4 |
También podemos comprobar esta propiedad de los triángulos rectángulos sin utilizar cuadrados (5) .
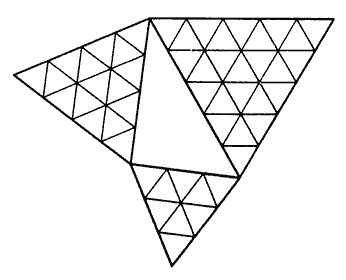
| Fig. 5 |
Tracemos triángulos equiláteros sobre los lados de un triángulo ABC dado, uno de cuyos ángulos ( C ) sea de 60° (6). El área conjunta del triángulo ABC primitivo y del triángulo opuesto a C es igual al área conjunta de los restantes triángulos. Demostración (7) : 1 + 2 + 3 = 1'+ 2'+ 3'.
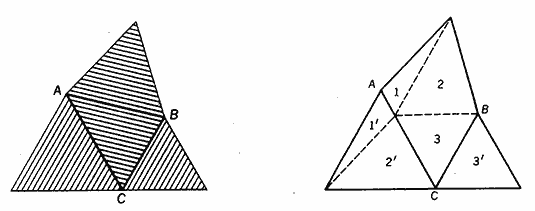
|
Fig. 6 | Fig. 7 |
Para trazar un triángulo equilátero podemos partir de un triángulo cualquiera, y trisecar sus ángulos: el pequeño triángulo así determinado en el centro del primero es equilátero (8) .
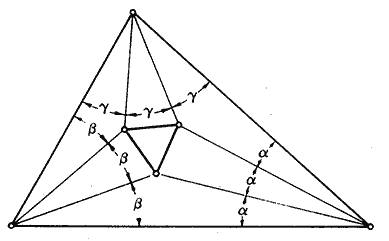
| Fig. 8 |
La trisección de un ángulo (su división en tres partes iguales) lo logra con mucha precisión bisecándolo primero (9) y dividiendo después la cuerda de cada semi-ángulo en tres partes iguales. El radio que corta a la cuerda a 2/3 de su extremo triseca el ángulo. La construcción sólo es aproximada.
Página siguiente



















