Michael Holt
Matemáticas recreativas 3
Título original: More Math Puzzles and Gantes, publicado por Walker and Company, Nueva York.
Traducción de M. Taboada
Ilustraciones de Pat Hickman
Cubierta: Geest/Hoverstad
Edición digital: Sargont (2019)
© by Michael Holt
© 1988, Ediciones Martínez Roca, S. A. – Barcelona
ISBN 84-270-1195-4
Depósito legal B. 5.855-1988
Impreso en España — Printed in Spain
Introducción
En este libro de pasatiempos y juegos matemáticos he incluido rompecabezas para que te diviertas con ellos y acaso también para que te instruyas un poco. La mayoría de estos pasatiempos no necesitan para resolverlos más que efectuar algunos cálculos con lápiz y papel, aunque, como es natural, no viene mal tratar de resolverlos mentalmente. Añadiré que ninguno de ellos precisa de dotes especiales. Basta con un poco de paciencia y una pizca de sentido común.
He añadido además ejemplos de la mayoría de los pasatiempos más conocidos, desde el clásico cruce de ríos hasta las absurdas invenciones de Lewis Carroll. Lo mismo que en el caso de mi anterior libro de pasatiempos matemáticos, debo mucho en éste a dos grandes especialistas, el americano Sam Loyd y su rival inglés Henry Dudeney.
No obstante, pertenezcan al tipo que pertenezcan, para su resolución no se necesitan conocimientos particulares. De hecho, requieren simplemente algunas dotes de deducción, un trabajo de lógica detectivesca.
Este libro termina con una serie de juegos matemáticos. Uno de los más sencillos, el «mancala», data de tiempos muy remotos, aunque se sigue jugando hoy en día en las aldeas africanas. Lo he visto jugar personalmente en Kenia. El llamado «sipu», igualmente sencillo, procede de Sudán. Ambos presentan sutilezas intrigantes, que descubrirás a medida que vayas jugando. He incluido asimismo una selección diversa de juegos de competición. Algunos de ellos están tomados del excelente libro de Boris A. Kordemsky, Moscow Puzzles: Three Hundred Fifty-Nine Mathematical Recreations. Sin embargo, el más original de todos, la división de un área triangular en tres, me lo enseñó un estudiante japonés, que lo jugaba con unos chiquillos en el campo de juegos de un parque de Londres.
Unas palabras sobre la solución de los problemas difíciles. Como ya dije anteriormente, si te atascas, no renuncies y te apresures a mirar la solución. Con eso no lograrás más que estropearte la diversión. Por regla general, doy generosas pistas que te pondrán en el buen camino. Si dichas pistas no te ayudan, deja de momento el problema. Tal vez más tarde se te ocurra una nueva línea de ataque. Intenta resolver un pasatiempo más fácil, aunque similar a aquel en el que te has atascado. Otro sistema consiste en conjeturar soluciones, para ver cuál de ellas tiene sentido. Con un poco de suerte, darás con la respuesta buena. De todos modos, convengo en que resolver los pasatiempos por chiripa no resulta tan satisfactorio como conseguirlo mediante un razonamiento paso a paso.
Si verdaderamente te ves en la imposibilidad de solucionarlo, mira la respuesta, pero, al principio, limítate a echar una ojeada a las primeras líneas. Quizá te proporcionen la pista que necesitas, sin que te aclaren todo el problema. Como observarás, se incluyen explicaciones muy completas para los problemas más difíciles o para aquellos que necesitan resolverse en varios pasos, es decir, para aquellos demasiado desconcertantes para comprenderlos a partir simplemente de la solución, sin añadir ninguna indicación de cómo se llegó a ella.
No obstante, resuelve los pasatiempos y elige los juegos a tu capricho. Espero que te diviertas mucho con ellos.
MICHAEL HOLT
Primera parte
Problemas
1. Formas planas y sólidas
Todos estos pasatiempos se refieren a formas planas dibujadas sobre papel o a formas sólidas. Precisan muy pocos conocimientos de geometría y pueden resolverse por simple sentido común o con un poco de experimentación. Algunos, por ejemplo, consisten en doblar papel. El camino más fácil para resolverlos consiste en tomar una hoja de papel, doblarla y cortarla. Otros exigen un poco de imaginación. Hay que visualizar un cubo o ver si coinciden ciertas formas sólidas en apariencia dispares. Uno o dos de ellos parecen exigir, a primera vista, conocimientos profundos de geometría. Cuando te ocurra eso, míralo más a fondo. Tal vez tenga una solución sencillísima. Sólo uno de los pasatiempos es casi un truco. Para la mayor parte de ellos basta con disponer de otro modo las formas o con recortarlas sobre papel.
1 La venta de solares
La Agencia Inmobiliaria Universal, los corredores de fincas más astutos del Oeste de los Estados Unidos, pusieron a la venta un pequeño solar triangular, situado en la calle Mayor de la parte más cara del área comercial correspondiente a la zona residencial de una ciudad americana. El espabilado agente de la Universal hizo publicar el anuncio siguiente en el periódico local:
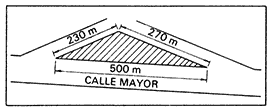
SE VENDE MAGNÍFICO LOTE DE TERRENO IDEAL PARA ALMACENES U OFICINAS
Subasta el 1 de abril
¿Por qué crees que no se presentaron compradores?
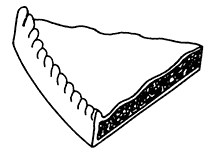
2 Los tres trozos de tarta
¿Se puede cortar este trozo triangular de tarta de manzana en tres partes iguales, todas de la misma forma y tamaño? La solución es fácil. Empieza por separar el borde con un corte recto y prescinde de él.
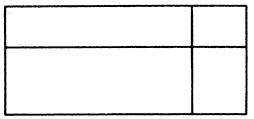
3 ¿Cuántos rectángulos?
¿Cuántos rectángulos hay en la figura siguiente?
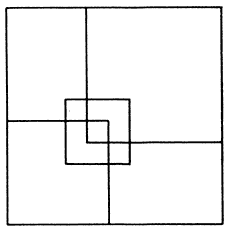
4 Los cuadrados
¿Cuántos cuadrados puedes señalar en el grabado? Recuerda que algunos de ellos forman parte de otros cuadrados mayores.
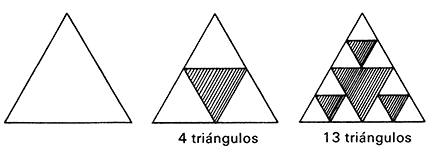
5 El triángulo triplicado
Copia el triángulo en blanco del grabado. Divídelo en triángulos más pequeños dibujando un triángulo sombreado en el centro. Con ello, tendrás un total de cuatro triángulos. Dibuja a continuación otros triángulos sombreados en cada uno de los que quedan en blanco, obteniendo así trece triángulos. Repite una vez más el proceso. ¿Cuántos triángulos sombreados y cuántos triángulos en blanco quedarán al final? ¿Has descubierto la pauta que siguen ambos números de triángulos? ¿Cuántos triángulos resultarán de las divisiones posteriores, sin necesidad de dibujarlos?
6 Los cuatro arbustos
¿Podrías plantar cuatro arbustos de manera que hubiese la misma distancia entre todos ellos? ¿Cómo lo harías?
INDICACIÓN : La forma cuadrada no sirve, ya que en ese caso habría más distancia entre los situados en diagonal que entre los situados formando lado.
7 El triángulo bromista
Resulta fácil descubrir los cinco triángulos en el triángulo de la izquierda. ¿Pero cuántos hay en el triángulo a y en el triángulo b ?